题目内容
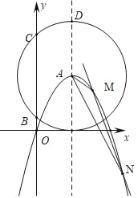
【题目】如图，在平面直角坐标系中，点A、B的坐标分别为
，
，点M是AO中点，
的半径为2．
若
是直角三角形，则点P的坐标为______
直接写出结果
若
，则BP与有怎样的位置关系？为什么？
若点E的坐标为
，那么上是否存在一点P，使
最小，如果存在，求出这个最小值，如果不存在，简要说明理由．
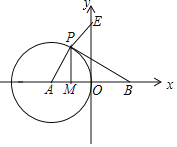
【答案】
或
或
或
；（2）详见解析；（3）
，
的最小值为
．
【解析】
（1）分两种情形：
，
分别求解即可解决问题；
（2）求出PA，PB的长，利用勾股定理的逆定理证明即可；
（3）如图3中，连接EM由
∽
，推出
，推出
，
，由
，，推出
的最小值为线段EM的长由此即可解决问题；
解：
设
，
如图1，当时，
的半径为2，且
，
点
，
；
如图2，当，
，
，
，
，
，
由
得
由
得到：
，
，
或
故答案为
或或或
如图2中，
，
，
在
中，
，
，
，
，
在
中，
，
，
，
，
，
是直角三角形．
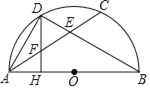
如图3中，连接EM．
，
，
，
，
，
∽，
，
，
，
，
的最小值为线段EM的长，
，
，
，
的最小值为．
练习册系列答案
相关题目
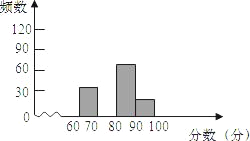
【题目】某校举行手工制作比赛，赛后整理参赛同学的成绩，并制作成图表如下：
分数段 | 频数 | 频率 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | m | 0.45 |
80≤x＜90 | 60 | n |
90≤x＜100 | 20 | 0.1 |
请根据以上图表提供的信息，解答下列问题：
（1）表中m和n所表示的数分别为：m＝______，n＝______，
（2）请在图中，补全频数分布直方图；
（3）比赛成绩的中位数落在哪个分数段？
（4）如果比赛成绩80分以上（含80分）可以获得奖励，那么获奖率是多少？
