题目内容
如果将线段所围成的封闭图形称之为一个区域，线段与线段的交点称之为顶点，围成封闭图形的线段称之为区域的边，那么在图形中其顶点数、边数以及区域数之间也存在奇妙的关系．例如，图形“△”的区域数为1，顶点数为3，边数为3；图形“
”的区域数为3，顶点数为4，边数为6，依此类推．
（1）请分别指出下列图形中的顶点数、区域数以及边数，并将相关数据填入下表中：
（2）根据上表的最后一列，你能归纳出什么结论？
（3）利用你归纳出的结论求：已知一个平面图形有50个顶点，48个区域，那么这个图形有多少条边？
”的区域数为3，顶点数为4，边数为6，依此类推．（1）请分别指出下列图形中的顶点数、区域数以及边数，并将相关数据填入下表中：
| 图形 | 顶点数（n） | 区域数（m） | 边数（f） | n+m-f |
| ① | ||||
| ② | ||||
| ③ | ||||
| ④ | ||||
| ⑤ |
（3）利用你归纳出的结论求：已知一个平面图形有50个顶点，48个区域，那么这个图形有多少条边？
分析：（1）利用已知图形分别得出定点数以及区域数和边数即可；
（2）利用图表中数据直接得出答案；
（3）利用（2）中规律得出f的值即可．
（2）利用图表中数据直接得出答案；
（3）利用（2）中规律得出f的值即可．
解答：解：（1）如下表：
（2）利用图表直接得出：n+m-f=1；
（3）∵一个平面图形有50个顶点，48个区域，n+m-f=1
∴50+48-f=1，
解得：f=97．
答：这个图形有97条边．
| 图形 | 顶点数（n） | 区域数（m） | 边数（f） | n+m-f |
| ① | 4 | 1 | 4 | 1 |
| ② | 6 | 2 | 7 | 1 |
| ③ | 5 | 3 | 7 | 1 |
| ④ | 9 | 4 | 12 | 1 |
| ⑤ | 8 | 5 | 12 | 1 |
（3）∵一个平面图形有50个顶点，48个区域，n+m-f=1
∴50+48-f=1，
解得：f=97．
答：这个图形有97条边．
点评：此题主要考查了图形的变化类，根据已知得出数字的变化规律是解题关键．
练习册系列答案
相关题目
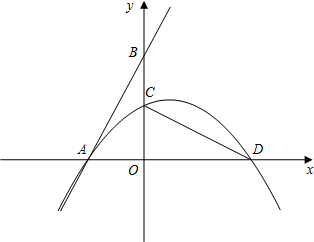
在平面直角坐标系中，如果横坐标与纵坐标都是整数的点称为整点，将二次函数y=-x2+6x-
的图象与x轴所围成的封闭图形染成红色，则在此红色区域内部及其边界上的整点的个数是（ ）
| 27 |
| 4 |
| A、5 | B、6 | C、7 | D、8 |
如果将线段所围成的封闭图形称之为一个区域，线段与线段的交点称之为顶点，围成封闭图形的线段称之为区域的边，那么在图形中其顶点数、边数以及区域数之间也存在奇妙的关系．例如，图形“△”的区域数为1，顶点数为3，边数为3；图形“
”的区域数为3，顶点数为4，边数为6，依此类推．
（1）请分别指出下列图形中的顶点数、区域数以及边数，并将相关数据填入下表中：
| 图形 | 顶点数（n） | 区域数（m） | 边数（f） | n+m-f |
| ① | ||||
| ② | ||||
| ③ | ||||
| ④ | ||||
| ⑤ |
（3）利用你归纳出的结论求：已知一个平面图形有50个顶点，48个区域，那么这个图形有多少条边？