Question

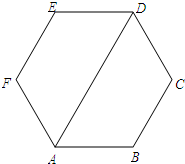如图，六边形ABCDEF的内角都相等，∠DAB=60°．
（1）写出四边形ADEF各内角的度数；
（2）探究图中哪些线段有平行关系（至少写3组），并选择其中一组说明理由．

Answer 1

解：（1）∵六边形ABCDEF的每个内角的度数是120°，∠DAB=60°．
∴∠E=∠F=120°，∠ADE=360°-2×120°-60°=60°，
∴∠FAD=360°-120°-120°-60°=60°．

（2）∵∠BAD=120°-∠FAD=60°
∴∠BAD=∠ADE=60°
∴AB∥DE．
同理可证CD∥AF．
与BC平行的线段有AD，EF．
证明：∵∠B+∠BAD=180°，
∴BC∥AD．
∵∠ADE+∠E=180°，
∴AD∥EF．
∴BC∥AD∥EF．
分析：（1）先求六边形ABCDEF的每个内角的度数，由于∠DAB=60°，可知∠DAF的度数，再根据四边形的内角和是360°，求∠ADE的度数，从而求解．
（2）由（1）中求出的度数，利用内错角相等，两直线平行，可证AB∥DE，CD∥AF．利用同旁内角互补两直线平行和平行于同一条直线的两直线平行，可得与BC平行的线段．
点评：考查了多边形内角与外角和平行线的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．注意平行于同一条直线的两直线平行．