题目内容
在△ABC中，D是BC的中点，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF。
【小题1】求证：AF=DC；
【小题2】如果AB=AC，试猜想四边形ADCF的形状，并证明。
【小题1】证明：∵AF∥BC，
∴∠AFE=∠DBE，∠FAE=∠BDE
∵ E是AD的中点，
∴ AE=DE，
∴△AEF≌△DEB，…
∴ AF=BD，…
∵ D是BC的中点，
∴ BD =DC，
∴ AF=DC。
【小题1】若AB=AC，则四边形ADCF是矩形。证明如下：
由（1）得AF AF∥DC，AF=DC，
∴四边形ADCF是平行四边形,
∵ AB=AC，且D是BC的中点，
∴ AD⊥BC,
∴∠ADC = 900，
∴四边形ADCF是矩形。
解析【小题1】因为BD=DC，要证明AF=CD，只需要证明BD=AF，由AF∥BD，AE=ED，
可证明△AEF≌△DEB．
【小题1】由（1）可知BD=DC，如果AB=AC，则AD⊥DC，四边形ADCF为矩形．
练习册系列答案
快乐5加2金卷系列答案
相关题目
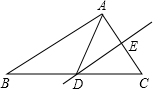如图所示，在△ABC中，DE是AC的中垂线，AE=3cm，△ABD得周长为13cm，则△ABC的周长是
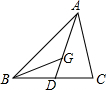如图，在△ABC中，AD是中线，G是重心，
如图在△ABC中，AD是BC边上的高，BE平分∠ABD，交AD于E．已知∠BED=60°，∠BAC=50°，则∠C=（ ）