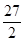题目内容
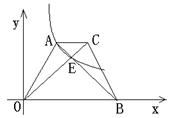
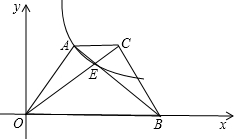 如图,梯形AOBC中,对角线交于点E,双曲线y=
如图,梯形AOBC中,对角线交于点E,双曲线y=| k |
| x |
分析:设△ACE的面积为S,则可得出△BOE的面积为9S,△AOE的面积为3S,△CEB的面积为3S,从而求出S,也可得出△OEB的面积,过点E作EF⊥OB,过点A作AM⊥OB于点M,设△OAM的面积为a,则△OEF的面积也为a,利用△BEF∽△BAM可得出a的值,则可得出△OEF的面积,也即可得出k的值.
解答:解:过点E作EF⊥OB于点F,过点A作AM⊥OB于点M,
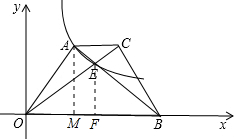
∵四边形AOBC是梯形,AC∥OB,AC:OB=1:3,
∴CE:EO=1:3,AE:EB=1:3,
设△ACE的面积为S,则可得出△BOE的面积为9S,△AOE的面积为3S,△CEB的面积为3S,
又∵梯形AOBC面积为24,
∴S+9S+3S+3S=24,
解得:S=
,
设△OAM的面积为a,则△OEF的面积也为a,
故可得△AMB的面积=18-a,△EFB的面积=
-a,
从而可得
=(
)2,即
=
,
解得:a=
,即S△AOM=S△OEF=
,
故可得k=2×
=
.
故选A.

∵四边形AOBC是梯形,AC∥OB,AC:OB=1:3,
∴CE:EO=1:3,AE:EB=1:3,
设△ACE的面积为S,则可得出△BOE的面积为9S,△AOE的面积为3S,△CEB的面积为3S,
又∵梯形AOBC面积为24,
∴S+9S+3S+3S=24,
解得:S=
| 3 |
| 2 |
设△OAM的面积为a,则△OEF的面积也为a,
故可得△AMB的面积=18-a,△EFB的面积=
| 27 |
| 2 |
从而可得
| S△BEF |
| S△ABM |
| BE |
| AB |
| ||
| 18-a |
| 9 |
| 16 |
解得:a=
| 54 |
| 7 |
| 54 |
| 7 |
故可得k=2×
| 54 |
| 7 |
| 108 |
| 7 |
故选A.
点评:此题属于反比例函数的综合题,涉及了相似三角形的性质,解答本题关键是掌握相似比等于面积比的平方,另外求出各部分的面积是本题的难点,注意掌握反比例函数的k的几何意义,难度较大.

练习册系列答案
相关题目
 如图,梯形AOBC中,AC∥OB,AO⊥OB,OA=2,OB=5,tanB是方程2x2+7x-4=0的一个根,以O为坐标原点,OB、OA所在的直线分别为x轴,y轴建立平面直角坐标系:
如图,梯形AOBC中,AC∥OB,AO⊥OB,OA=2,OB=5,tanB是方程2x2+7x-4=0的一个根,以O为坐标原点,OB、OA所在的直线分别为x轴,y轴建立平面直角坐标系: 如图,梯形AOBC中,AC∥OB,AO⊥OB,OA=2,OB=5,tanB是方程2x2+7x-4=0的一个根,以O为坐标原点,OB、OA所在的直线分别为x轴,y轴建立平面直角坐标系:
如图,梯形AOBC中,AC∥OB,AO⊥OB,OA=2,OB=5,tanB是方程2x2+7x-4=0的一个根,以O为坐标原点,OB、OA所在的直线分别为x轴,y轴建立平面直角坐标系:
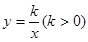 经过A、E两点,若AC:OB=1:3,梯形AOBC面积为24,则k=(
)
经过A、E两点,若AC:OB=1:3,梯形AOBC面积为24,则k=(
)
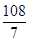 B、
B、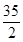 C、
C、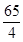 D、
D、