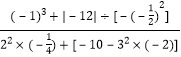题目内容
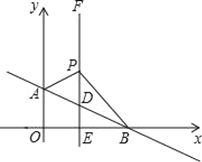
【题目】如图,正方形OABC的顶点O在坐标原点,顶点A的坐标为(4,3) 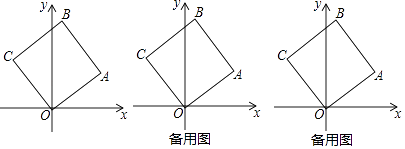
(1)顶点C的坐标为( , ),顶点B的坐标为( , );
(2)现有动点P、Q分别从C、A同时出发,点P沿线段CB向终点B运动,速度为每秒1个单位,点Q沿折线A→O→C向终点C运动,速度为每秒k个单位,当运动时间为2秒时,以P、Q、C为顶点的三角形是等腰三角形,求此时k的值.
(3)若正方形OABC以每秒 ![]() 个单位的速度沿射线AO下滑,直至顶点C落到x轴上时停止下滑.设正方形OABC在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
个单位的速度沿射线AO下滑,直至顶点C落到x轴上时停止下滑.设正方形OABC在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
【答案】
(1)﹣3;4;1;7
(2)
解:由题意得,AO=CO=BC=AB=5,
当t=2时,CP=2.
①当点Q在OA上时,∵PQ≥AB>PC,
∴只存在一点Q,使QC=QP.
作QD⊥PC于点D(如图2中),则CD=PD=1,
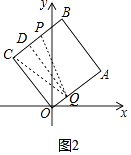
∴QA=2k=5﹣1=4,
∴k=2.②当点Q在OC上时,由于∠C=90°所以只存在一点Q,使CP=CQ=2,
∴2k=10﹣2=8,∴k=4.
综上所述,k的值为2或4
(3)
解:①当点A运动到点O时,t=3.
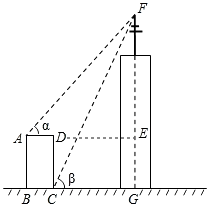
当0<t≤3时,设O’C’交x轴于点E,作A’F⊥x轴于点F(如图3中).
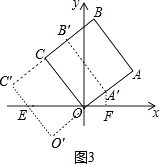
则△A’OF∽△EOO’,
∴ ![]() =
= ![]() =
= ![]() ,OO′=
,OO′= ![]() t,
t,
∴EO′= ![]() t,
t,
∴S= ![]() t2.②当点C运动到x轴上时,t=4
t2.②当点C运动到x轴上时,t=4
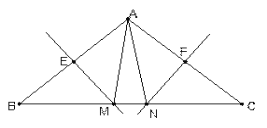
当3<t≤4时(如图4中),设A’B’交x轴于点F,
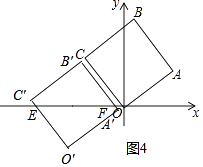
则A’O=A′O= ![]() t﹣5,
t﹣5,
∴A′F= ![]() .
.
∴S= ![]() (
( ![]() +
+ ![]() t)×5=
t)×5= ![]() .
.
综上所述,S= 
【解析】解:(1)如图1中,作CM⊥x轴于,AN⊥x轴于N.连接AC、BO交于点K.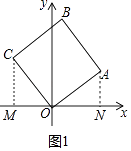
易证△AON≌△COM,可得CM=ON=4,OM=AN=3,
∴C(﹣3,4),∵CK=AK,OK=BK,
∴K( ![]() ,
, ![]() ),B(1,7),
),B(1,7),
所以答案是﹣3,4,1,7
【考点精析】本题主要考查了正方形的性质和坐标与图形变化-平移的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能正确解答此题.