题目内容
如图，在⊙O中，弦AB=2，CD=1，AD⊥BD，直线AD、BC相交于点E，求∠E的度数。
解：连结OC、OD
∵ AD⊥BD，即∠ADB=90°
∴ AB是⊙O的直径
∵ AB=2
∴ OC=OD=
AB=
×2=1
∵ CD=1
∴△DOC是等边三角形
∵∠DOC=60°
∴∠DBE=∠DOC=
×60°=30°
∵在Rt△EDB中∠EDB=90°
∴ ∠E=90°-30°=60°。
∵ AD⊥BD，即∠ADB=90°
∴ AB是⊙O的直径
∵ AB=2
∴ OC=OD=
AB=×2=1∵ CD=1
∴△DOC是等边三角形
∵∠DOC=60°
∴∠DBE=∠DOC=
×60°=30°∵在Rt△EDB中∠EDB=90°
∴ ∠E=90°-30°=60°。
练习册系列答案
相关题目
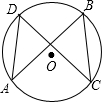已知：如图，在⊙O中，弦AD=BC．求证：AB=CD．
4、如图，在⊙O中，弦BC∥半径OA，AC与OB相交于M，∠C=20°，则∠AMB的度数为（ ）
标系．
如图，在⊙O中，弦AB=BC=CD，且∠ABC=140°，则∠AED=（ ）
如图，在⊙O中，弦AB与CD相交于点P，连接AC、DB．