题目内容
如图,已知直线l1:y=2x+3,直线l2:y=-x+5,直线l1、l2分别交x轴于B、C两点,l1、l2相交于点A.(1)求A、B、C三点坐标;
(2)求△ABC的面积.

【答案】分析:(1)首先分别令直线l1、直线l2中的y为0.即可得B、C点的坐标,因为l1、l2相交于点A,所以联立方程①②即可解得A点坐标.
(2)由函数图象可得S△ABC= ×|BC|×|yA|,根据(1)中坐标即可求得面积.
×|BC|×|yA|,根据(1)中坐标即可求得面积.
解答:解:(1)由题意得,令直线l1、直线l2中的y为0,得:x1=- ,x2=5,
,x2=5,
由函数图象可知,点B的坐标为(- ,0),点C的坐标为(5,0),
,0),点C的坐标为(5,0),
∵l1、l2相交于点A,
∴解y=2x+3及y=-x+5得:x= ,y=
,y= ,
,
∴点A的坐标为( ,
, );
);
(2)由(1)题知:|BC|= ,
,
又由函数图象可知S△ABC= ×|BC|×|yA|=
×|BC|×|yA|= ×
× ×
× =
= .
.
点评:本题考查了一次函数图象上点的坐标特征,是常考题型,要注意掌握.
(2)由函数图象可得S△ABC=
 ×|BC|×|yA|,根据(1)中坐标即可求得面积.
×|BC|×|yA|,根据(1)中坐标即可求得面积.解答:解:(1)由题意得,令直线l1、直线l2中的y为0,得:x1=-
 ,x2=5,
,x2=5,由函数图象可知,点B的坐标为(-
 ,0),点C的坐标为(5,0),
,0),点C的坐标为(5,0),∵l1、l2相交于点A,
∴解y=2x+3及y=-x+5得:x=
 ,y=
,y= ,
,∴点A的坐标为(
 ,
, );
);(2)由(1)题知:|BC|=
 ,
,又由函数图象可知S△ABC=
 ×|BC|×|yA|=
×|BC|×|yA|= ×
× ×
× =
= .
.点评:本题考查了一次函数图象上点的坐标特征,是常考题型,要注意掌握.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 6、如图,已知直线l1,l2,l3相交于点O,∠1=35°,∠2=25°,则∠3等于( )
6、如图,已知直线l1,l2,l3相交于点O,∠1=35°,∠2=25°,则∠3等于( ) (2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
(2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )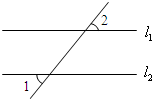 (2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2=
(2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2= 如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.
如图:已知直线l1∥l2,且l3、l4和l1、l2分别交于点A、B和点C、D,点P在AB上,设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.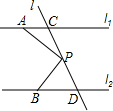 如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.