Question

【题目】如图1，正方形ABCD的边长为4厘米，E为AD边的中点，F为AB边上一点，动点P从点B出发，沿B→C→D→E，向终点E以每秒a厘米的速度运动，设运动时间为t秒，△PBF的面积记为S. S与t的部分函数图象如图2所示，已知点M（1， ）、N（5，6）在S与t的函数图象上.

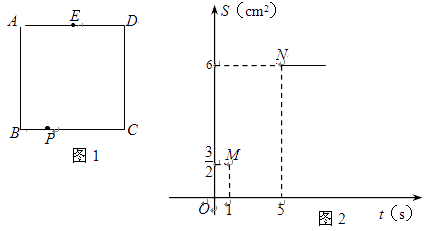
（1）求线段BF的长及a的值；
（2）写出S与t的函数关系式，并补全该函数图象；
（3）当t为多少时，△PBF的面积S为4.

Answer 1

【答案】
（1）解：由题意可知，当t=5时，S△PBF= ×4BF=6，BF=3.当t=1时，S△PBF= at×3= ，a=1


（2）解：当0≤t≤4时，设S=kt，把（1， ）代入得，k= ，S= t；当4＜t≤8时，S=6；当8＜t≤10时，设S=mt+b，把（8,6），（10,3）代入，得 ，解得 ，S=18- t.综上所述，当0≤t≤4时，S= t；当4＜t≤8时，S=6；当8＜t≤10时，S=18- t，据此可补全图像，如下图：

（3）解：当S＝4时， t＝4，t＝ ；18－ t＝4，t＝ .∴当t＝ 或 t＝ 时△PBF的面积S为4
【解析】（1）根据t=5时S=6求出BF的长，根据t=1时S= 列式可计算出a的值；
（2）S与t的函数关系式分以下三种情况：
①点P在BC上运动时，即0≤t≤4；
②点P在CD边上运动，即4<t≤8；
③点P在线段DE上运动时，即8<t≤10，分别按照三角形面积公式列出函数表达式．
（3）把S=4分别代入S=t,和s=18-t,求得t的值即可。