题目内容
四边形ABCD中，AD=BC，P、E、F为BD、AB、CD中点，∠PEF=20°，∠EPF=________．
140°
分析：根据三角形的中位线平行于第三边并且等于第三边的一半可得PE=
AD，PF=BC，从而求出PE=PF，根据等边对等角可得∠PFE=∠PEF，然后根据三角形的内角和定理列式计算即可得解．
解答：
解：∵P、E、F为BD、AB、CD中点，
∴PE、PF分别是△ABD和△BCD的中位线，
∴PE=AD，PF=BC，
∵AD=BC，
∴PE=PF，
∴∠PFE=∠PEF=20°，
在△PEF中，∠EPF=180°-20°×2=140°．
故答案为：140°．
点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等腰三角形的性质，以及三角形的内角和定理，熟记定理与性质是解题的关键，作出图形更形象直观．
分析：根据三角形的中位线平行于第三边并且等于第三边的一半可得PE=
AD，PF=BC，从而求出PE=PF，根据等边对等角可得∠PFE=∠PEF，然后根据三角形的内角和定理列式计算即可得解．解答：
解：∵P、E、F为BD、AB、CD中点，∴PE、PF分别是△ABD和△BCD的中位线，
∴PE=
AD，PF=BC，∵AD=BC，
∴PE=PF，
∴∠PFE=∠PEF=20°，
在△PEF中，∠EPF=180°-20°×2=140°．
故答案为：140°．
点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等腰三角形的性质，以及三角形的内角和定理，熟记定理与性质是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
23、如图，四边形ABCD中，对角线AC、BD相交于点E．已知：DA=DC，E为AC中点．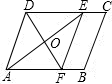
如图所示，在平行四边形ABCD中，AE是∠DAB的平分线，EF∥AD交AB于点F，若AB=9，CE=4，AE=8，则DF等于（ ）
17、如图，在平行四边形ABCD中，对角线AC、BD相交于点O，过点O的直线EF分别交AB、CD于E、F．请写出图中三对全等的三角形：
7、如图，在四边形ABCD中，AD=CB，∠ACB=∠CAD．求证：AB=CD．