题目内容
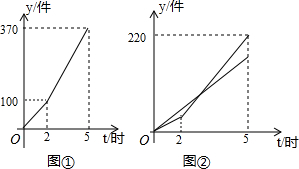 有一项工作,由甲、乙合作完成,合作一段时间后,乙改进了技术,提高了工作效率.图①表示甲、乙合作完成的工作量y(件)与工作时间t(时)的函数图象.图②分别表示甲完成的工作量y甲(件)、乙完成的工作量y乙(件)与工作时间t(时)的函数图象,则甲每小时完成
有一项工作,由甲、乙合作完成,合作一段时间后,乙改进了技术,提高了工作效率.图①表示甲、乙合作完成的工作量y(件)与工作时间t(时)的函数图象.图②分别表示甲完成的工作量y甲(件)、乙完成的工作量y乙(件)与工作时间t(时)的函数图象,则甲每小时完成30
30
件,乙提高工作效率后,再工作| 2 |
| 3 |
| 2 |
| 3 |
分析:根据图象可以设甲原来每小时做x件,乙每小时作y件,乙提高工作效率后每小时比原来多做a件,根据函数图象建立方程组就可以求出x、y的值,再设乙提高工作效率后再工作m小时与甲完成的工作量相等建立方程求出m的值即可.
解答:解:设甲原来每小时做x件,乙每小时作y件,乙提高工作效率后每小时比原来多做a件,由图象,得
,
解得:
,
则甲每小时完成30件;
设乙提高工作效率后再工作m小时与甲完成的工作量相等,由题意,得
2×20+(20+40)m=2×30+30m,
解得:m=
,
故答案为:30,
.
|
解得:
|
则甲每小时完成30件;
设乙提高工作效率后再工作m小时与甲完成的工作量相等,由题意,得
2×20+(20+40)m=2×30+30m,
解得:m=
| 2 |
| 3 |
故答案为:30,
| 2 |
| 3 |
点评:本题考查了一次函数的运用,工程问题在解实际问题中的运用,解答时认真理解函数图象的含义是解答本题的关键.

练习册系列答案
相关题目
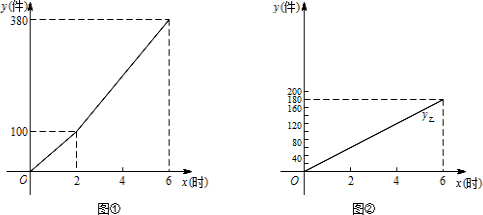
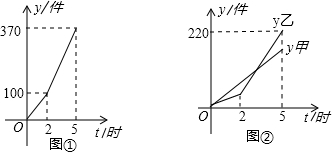 工作量y乙(件)与工作时间t(时)的函数图象.
工作量y乙(件)与工作时间t(时)的函数图象.
