题目内容
如图,在平行四边形ABCD中,点G是BC延长线上一点,AG与BD交于点E,与DC交于点F,如果AB=m,CG= BC,
BC,

求:(1)DF的长度;
(2)三角形ABE与三角形FDE的面积之比.
(1) ;(2)9:4.
;(2)9:4.
【解析】
试题分析:(1)根据四边形ABCD是平行四边形,得出AB∥CD,然后根据平行线分线段成比例定理可得CF,DF与AB的关系;(2)利用相似三角形的性质,面积的比等于相似比的平方,可得出结论.
试题解析:【解析】
(1)∵四边形ABCD是平行四边形,
∴AB=CD=m,AB∥CD.∵CG= BC,∴CG=
BC,∴CG= BG,
BG,
∵AB∥CD,∴ .∴
.∴ ,∴
,∴ ; 5分
; 5分
(2)∵AB∥CD,∴△ABE∽△FDE,
∴ .∴△ABE与△FDE的面积之比为9:4. 8分
.∴△ABE与△FDE的面积之比为9:4. 8分
考点:1.平行四边形的性质;2.平行线分线段成比例定理;3.相似三角形的判定与性质.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 >0时,
>0时, 随
随 的增大而增
的增大而增 (
( ,
, )与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
)与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
 ,求反比例函数的解析式.
,求反比例函数的解析式. 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.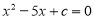 的一个根,则这个方程的另一个根是( )
的一个根,则这个方程的另一个根是( )
 ≈1.732)
≈1.732)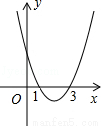
 (k≠0)在同一坐标系中的图象大致是( )
(k≠0)在同一坐标系中的图象大致是( )