题目内容
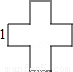
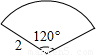
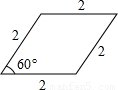
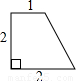
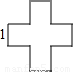
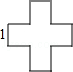
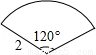
连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( )
|
| A. |
| B. |
| C. |
| D. |
|
考点:
菱形的性质;勾股定理;直角梯形.
分析:
先找出每个图形的“直径”,再根据所学的定理求出其长度,最后进行比较即可.
解答:
解: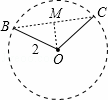
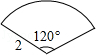
连接BC,则BC为这个几何图形的直径,过O作OM⊥BC于M
∵OB=OC,
∴∠BOM=![]() ∠BOC=60°,
∠BOC=60°,
∴∠OBM=30°,
∵OB=2,OM⊥BC,
∴OM=![]() OB=1,由勾股定理得:BM=
OB=1,由勾股定理得:BM=![]() ,
,
∴由垂径定理得:BC=2![]() ;
;
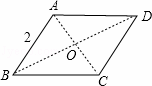
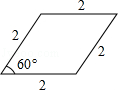
连接AC、BD,则BD为这个图形的直径,
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC,
∵∠ABC=60°,
∴∠ABO=30°,
∴AO=![]() AB=1,由勾股定理得:BO=
AB=1,由勾股定理得:BO=![]() ,
,
∴BD=2BO=2![]() ;
;
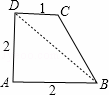
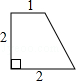
连接BD,则BD为这个图形的直径,
由勾股定理得:BD=![]() =2
=2![]() ;
;
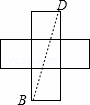
连接BD,则BD为这个图形的直径,
由勾股定理得:BD=![]() =
=![]() ,
,
∵2![]() >
>![]() >2
>2![]() ,
,
∴选项A、B、D错误,选项C正确;
故选C.
点评:
本题考查了菱形性质,勾股定理,含30度角的直角三角形性质,扇形性质等知识点的应用,主要考查学生的理解能力和推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 B.
B.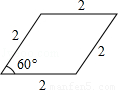 C.
C.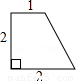 D.
D.