题目内容
绝对值小于5的所有的整数的和 。
0
【解析】
试题分析:绝对值小于0的整数有很多,其中有一个整数为0,任何数与0的乘积均为0,所以,所有整数的乘积为0,即得.
考点:1。绝对值的概念。2.有理数的乘法运算
考点分析: 考点1:有理数 1、有理数的概念:正数和分数统称为有理数.2、有理数的分类:
①按整数、分数的关系分类; ②按正数、负数与0的关系分类.
有理数{整数{正整数0负整数分数{正分数负分数 有理数 {正数{正整数正分数0负数{负整数负分数
注意:如果一个数是小数,它是否属于有理数,就看它是否能化成分数的形式,所有的有限小数和无限循环小数都可以化成分数的形式,因而属于有理数,而无限不循环小数,不能化成分数形式,因而不属于有理数. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
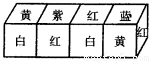
把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况列表如下:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 6 | 5 | 4 | 3 | 2 | 1 |
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如下图所示,那么长方体的下底面共有______朵花.
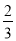 、9、
、9、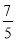 、-(-8)、0、-|+3|,负有理数有( )
、-(-8)、0、-|+3|,负有理数有( )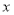 元,可得方程 .
元,可得方程 .
 是二次三项式
是二次三项式  不是单项式
不是单项式 的系数是
的系数是
 的次数是6
的次数是6 的顶点坐标是( )
的顶点坐标是( )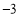 ) B、(
) B、(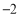 ,3) C、(2,3) D、(
,3) C、(2,3) D、(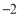 ,
,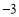 )
)