题目内容
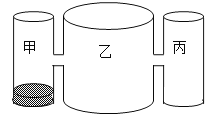
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面面积之比为1:4:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示,若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm.
cm.
求:(1)开始注水1分钟,丙容器的水位上升了多少?
(2)开始注入多少分钟的水量后,甲与乙的水位高度相差0.5cm?
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(1)由甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,注水1分钟,乙的水位上升![]() cm,得到注水1分钟,丙的水位上升
cm,得到注水1分钟,丙的水位上升![]() cm;
cm;
(2)设开始注入t分钟的水量后,乙的水位比甲高0.5cm,有两种情况:①甲的水位不变时,②乙的水位到达管子底部,甲的水位上升时,分别列方程求解即可;设开始注入a分钟的水量后,甲的水位比乙高0.5cm.
试题解析:(1)∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,
∵注水1分钟,乙的水位上升![]() cm,
cm,
∴得到注水1分钟,丙的水位上升![]() cm×4=
cm×4=![]() cm;
cm;
(2)设开始注入t分钟的水量后,乙的水位比甲高0.5cm,有两种情况:
①甲的水位不变时;
由题意得, ![]() t1=0.5,
t1=0.5,
解得:t=![]() ,
,
∵![]() ×
×![]() =6>5,
=6>5,
∴此时丙容器已向乙容器溢水,
∵5÷![]() =
=![]() 分钟,
分钟, ![]() ×
×![]() =
=![]() ,即经过
,即经过![]() 分钟时丙容器的水到达管子底部,乙的水位上升
分钟时丙容器的水到达管子底部,乙的水位上升![]() ,
,
∴![]() +2×
+2×![]() (t
(t![]() )1=0.5,解得:t=
)1=0.5,解得:t=![]() ;
;
②当乙的水位到达管子底部,甲的水位上升时,
∵乙的水位到达管子底部的时间为; ![]() +(5
+(5![]() )÷
)÷![]() ÷2=
÷2=![]() 分钟,
分钟,
∴512×![]() (t
(t![]() )=0.5,
)=0.5,
解得:t=![]() ,
,
综上所述开始注入![]() 或
或![]() 分钟的水量后,乙的水位比甲高0.5cm;
分钟的水量后,乙的水位比甲高0.5cm;
③设开始注入a分钟的水量后,甲的水位比乙高0.5cm,
由题意得:10.5=![]() a,
a,
解得:a=![]()
答:开始注入![]() ,40分钟的水量后,甲与乙的水位高度之差是0.5cm.
,40分钟的水量后,甲与乙的水位高度之差是0.5cm.

 阅读快车系列答案
阅读快车系列答案【题目】某鞋店销售一款新式女鞋,试销期间对该款不同型号的女鞋销售量统计如下表:
尺码/厘米 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
销售量/双 | 1 | 2 | 3 | 11 | 8 | 6 | 4 |
该店经理如果想要了解哪种女鞋的销售量最大,那么他应关注的统计量是_____.