题目内容
将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DCF的值是________.
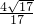
分析:首先根据题意画出图形,然后设AB=4x,AD=5x,由折叠的性质,可得DF=x,由勾股定理即可求得CF=
 x,继而求得cos∠DCF的值.
x,继而求得cos∠DCF的值.解答:
 解:∵AB:BC=4:5,
解:∵AB:BC=4:5,∴设AB=4x,AD=5x,
∵将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,
∴AF=AB,∠D=90°,AD=BC=5x,CD=AB=4x,
∴DF=AD-AF=5x-4x=x,
∴CF=
 =
= x,
x,∴cos∠DCF=
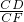 =
= =
=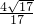 .
.故答案为:
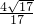 .
.点评:此题考查了折叠的性质、矩形的性质、勾股定理以及余弦函数的定义.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
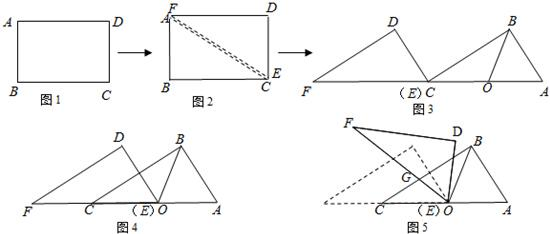
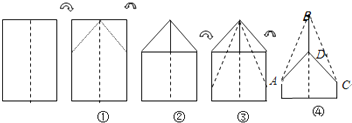
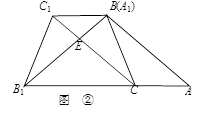
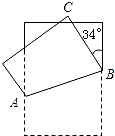 将一张矩形纸片折叠成如图所示的形状,则∠ABC=
将一张矩形纸片折叠成如图所示的形状,则∠ABC=