题目内容
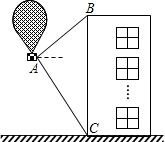2009年首届中国国际航空体育节在莱芜雪野举办，期间在市政府广场进行了热气球飞行表演．如图，有一热气球到达离地面高度为36米的A处时，仪器显示正前方一高楼顶部B的仰角是37°，底部C的俯角是60°．为了安全飞越高楼，气球应至少再上升多少米？（结果精确到0.1米）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，| 3 |
分析：过A作BC的垂线，设垂足为D．BD即为所求的高度．
在Rt△ADC中，运用三角函数定义求出AD的值；进而可在Rt△ABD中，求出BD的值．
在Rt△ADC中，运用三角函数定义求出AD的值；进而可在Rt△ABD中，求出BD的值．
解答：
解：过A作AD⊥CB，垂足为点D．
在Rt△ADC中，
∵CD=36，∠CAD=60°，
∴AD=
=
=12
≈20.76．
在Rt△ADB中，
∵AD≈20.76，∠BAD=37°，
∴BD=AD×tan37°≈20.76×0.75=15.57≈15.6．
答：气球应至少再上升15.6米．
解：过A作AD⊥CB，垂足为点D．在Rt△ADC中，
∵CD=36，∠CAD=60°，
∴AD=
| CD |
| tan60° |
| 36 | ||
|
| 3 |
在Rt△ADB中，
∵AD≈20.76，∠BAD=37°，
∴BD=AD×tan37°≈20.76×0.75=15.57≈15.6．
答：气球应至少再上升15.6米．
点评：本题考查仰角俯角的定义，要求学生能借助仰角俯角构造直角三角形并解直角三角形．
练习册系列答案
名校课堂系列答案
相关题目
）
）
）