��Ŀ����
ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�Ϊÿ��50Ԫ��ÿ���¿�����210�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������10����ÿ���ۼ۲��ܸ���65Ԫ����
��ÿ����Ʒ���ۼ�����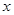 Ԫ��
Ԫ��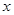 Ϊ����������ÿ���µ���������Ϊ
Ϊ����������ÿ���µ���������Ϊ Ԫ��
Ԫ��
��1���� ��
��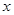 �ĺ�����ϵʽ��ֱ��д���Ա���
�ĺ�����ϵʽ��ֱ��д���Ա���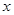 ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
��3��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���µ�����ǡΪ2200Ԫ���������Ͻ��ۣ�����ֱ��д���ۼ���ʲô��Χʱ��ÿ���µ�������2200Ԫ��
(1)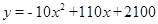 ��0��x��15��x��������(2)55��56,2400;
��0��x��15��x��������(2)55��56,2400;
(3) ,
, ,������51Ԫ�Ҳ�����60Ԫ��Ϊ����.
,������51Ԫ�Ҳ�����60Ԫ��Ϊ����.
���������������1�������۵���ÿ��1Ԫ���ͻ����۳�10��,��
��0��x��15��x��������
��2����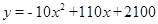 �����䷽����������ֵ�����������.
�����䷽����������ֵ�����������.
��3����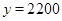 ʱ��
ʱ��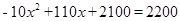 ����ã�
����ã� ,
, ��
��
�� ʱ��
ʱ�� ����
���� ʱ��
ʱ�� ��
��
���ۼ۶�Ϊÿ��51��60Ԫ��ÿ���µ�����Ϊ2200Ԫ��
�����������1�� ��
�� ��
�� ��������
��������
��2��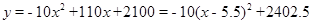 ��
��
��a=-10��0��
�൱x=5.5ʱ,y�����ֵ2402.5��
��0��x��15��x������
�൱x=5ʱ��50+x=55��y=2400��Ԫ������x=6ʱ��50+6=56��y=2400��Ԫ��
�൱�ۼ۶�Ϊÿ��55��56Ԫ��ÿ���µ��������������������2400Ԫ��
��3����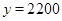 ʱ��
ʱ��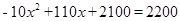 ����ã�
����ã� ,
, ��
��
�൱ ʱ��
ʱ�� ����
���� ʱ��
ʱ�� ��
��
�൱�ۼ۶�Ϊÿ��51��60Ԫ��ÿ���µ�����Ϊ2200Ԫ��
�൱�ۼ۲�����51��60Ԫ��ÿ���µ�����Ϊ2200Ԫ��
�൱�ۼ۲�����51Ԫ�Ҳ�����60Ԫ��Ϊ����ʱ��ÿ���µ�������2200Ԫ�����ۼ۷ֱ�Ϊ51��52��53��54��55��56��57��58��59��60Ԫʱ��ÿ���µ�������2200Ԫ����
���㣺1.���κ�����Ӧ�ã�2.һԪ���η��̵�Ӧ��.

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д� ��ͼ��Գ���Ϊ
��ͼ��Գ���Ϊ ���ҹ���B����1��0������˶��κ����ı���ʽ.
���ҹ���B����1��0������˶��κ����ı���ʽ.
 ��y�ύ�ڵ�A���������ϵ�һ��P�ڵ������ޣ�����AP��x�ύ�ڵ�C��
��y�ύ�ڵ�A���������ϵ�һ��P�ڵ������ޣ�����AP��x�ύ�ڵ�C�� ����S��AOC=1������P��PB��y���ڵ�B��
����S��AOC=1������P��PB��y���ڵ�B��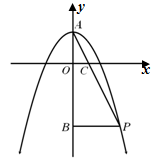

 ������(m��0)��(n��0)����
������(m��0)��(n��0)���� ����������˫����
����������˫���� ��x��0���Ľ���Ϊ��1��d����
��x��0���Ľ���Ϊ��1��d���� ����˫����
����˫���� ,OΪ����ԭ�㣬��
,OΪ����ԭ�㣬�� ,��Q��˫����
,��Q��˫���� ��
��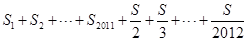 ��ֵ��
��ֵ��