Question

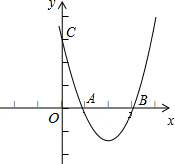已知：如图，抛物线y=ax²+bx+c与x轴相交于两点A（1，0），B（3，0）与y轴相交于点C（0，3），
（l）求抛物线的函数关系式；
（2）若点D（4，m）是抛物线y=ax²+bx+c上一点，请求出m的值，并求出此时△ABD的面积；
（3）若点A（x₁，y₁）、B（x₂，y₂）是该二次函数图象上的两点，且-1＜x₁＜0，1＜x₂＜2，试比较两函数值的大小：y₁______y₂；
（4）若自变量x的取值范围是0≤x≤5，则函数值y的取值范围是______．

Answer 1

解：（1）设二次函数解析式为y=a（x-1）（x-3），
将C（0，3）坐标代入得：3=3a，即a=1，
则二次函数解析式为y=（x-1）（x-3）=x²-4x+3；

（2）把D（4，m）代入解析式得：16-16+3=m，即m=3，
则S_△ABD=×（3-1）×3=3；

（3）∵二次函数的对称轴为直线x=2，
∴A与B都在对称轴左边，
∵-1＜x₁＜0，1＜x₂＜2，
∴x₁＜x₂，
∴y₁＞y₂；

（4）∵二次函数解析式为y=（x-2）²-1，
∴当x=2时，二次函数的最小值为-1，
又∵0≤x≤5，
∴x=0时，函数值为3；x=5时，函数值为8，
则此时函数值y的取值范围是-1≤y≤8．
故答案为：（3）＞；（4）-1≤y≤8
分析：（1）由二次函数与x轴的两交点A与B，设出二次函数的二根式方程，将C坐标代入求出a的值，即可确定出解析式；
（2）将D横坐标代入解析式中求出m的值，由A与B的坐标求出AB的长，为三角形ABD的底，高为D纵坐标的绝对值，利用三角形面积公式求出即可；
（3）由二次函数的对称轴为直线x=2，得到A与B在对称轴的左边，由抛物线开口向上，得到此时为减函数，由x₁＜x₂，即可得出y₁与y₂的大小关系；
（4）由抛物线开口向上有最小值，求出最小值，再将x=0与x=5分别代入求出对应的函数值，即可得出此时y的范围．
点评：此题考查了待定系数法确定二次函数解析式，二次函数的图象与性质，坐标与图形性质，以及三角形的面积，熟练掌握待定系数法是解本题的关键．