题目内容
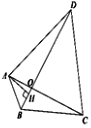
【题目】已知:四边形ABCD中,![]() ,
,![]() ,AD=CD,对角线AC,BD相交于点O,且BD平分∠ABC,过点A作
,AD=CD,对角线AC,BD相交于点O,且BD平分∠ABC,过点A作![]() ,垂足为H.
,垂足为H.
(1)求证:![]() ;
;
(2)判断线段BH,DH,BC之间的数量关系;并证明.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)首先证明△ADC是等边三角形,再证明∠DAO=∠CBO=60°,最后根据三角形内角和定理证明∠ADB=∠ACB;
(2)如图,在HD上截取HE=BH.首先证明△ABH≌△AEH,得出AB=AE,∠AEH=∠ABH=60°,再证明△ABC≌△AED,得出BC=ED,即可得出结论.
(1)证明:∵![]() ,
,![]() ∴
∴![]() 是等边三角形.
是等边三角形.![]() ,
,![]() .∵
.∵![]() ,BD平分
,BD平分![]() ,
,![]() .
.![]() ,∵
,∵![]() ,
,![]() ,
,![]()
![]()
(2)结论:![]() ;证明:在HD上截取
;证明:在HD上截取![]() ,如下图,
,如下图,
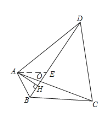
∵![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∵
,∵![]() ,
,![]() .
.

练习册系列答案
相关题目