��Ŀ����
�Ķ�����IJ���
��1����֪����y=3x-1
�⣺��y=3x-1���ɵ�x=
������ԭ����y=3x-1�ķ�������y=
��2����֪����y=
��x��1��
�⣺��y=
���ɵ�x=
������ԭ����y=
�ķ�������y=
��x��2��
�����������У�����Ӧ�������£�һ��ԭ�����з�����ʱ��ԭ�������Ա���x��ȡֵ��Χ�������ķ�������y�ĺ���ֵȡֵ��Χ��ԭ�����к���ֵy��ȡֵ��Χ�������ķ��������Ա���xȡֵ��Χ��ͨ���������������������
��1������y=-2x+3�ķ�������
��2������y=
�ķ������ĺ���ֵ��ȡֵ��ΧΪ
A��y��1 B��y��-1 C��y��-2 D��y��2��
��3������������������������
��y=x ��y=x+1 ��y=-x+1 ��y=
��y=
(x��1)��
��1����֪����y=3x-1
�⣺��y=3x-1���ɵ�x=
| y+1 |
| 3 |
| x+1 |
| 3 |
��2����֪����y=
| x+3 |
| x-1 |
�⣺��y=
| 2x+3 |
| x-1 |
| y+3 |
| y-2 |
| 2x+3 |
| x-1 |
| x+3 |
| x-2 |
�����������У�����Ӧ�������£�һ��ԭ�����з�����ʱ��ԭ�������Ա���x��ȡֵ��Χ�������ķ�������y�ĺ���ֵȡֵ��Χ��ԭ�����к���ֵy��ȡֵ��Χ�������ķ��������Ա���xȡֵ��Χ��ͨ���������������������
��1������y=-2x+3�ķ�������
��2������y=
| x-2 |
| x+1 |
B
B
A��y��1 B��y��-1 C��y��-2 D��y��2��
��3������������������������
�٢ܢ�
�٢ܢ�
������ż��ɣ���y=x ��y=x+1 ��y=-x+1 ��y=
| 1 |
| x |
| x+1 |
| x-1 |
��������1���������⣬����y��ʾ��x��Ȼ�ɵõ���������
��2��������Ŀ��Ϣ�����ԭ�������Ա�����ȡֵ��Χ��Ϊ�������ĺ���ֵ�ķ�Χ��
��3�����ݷ������Ķ���ֱ������С��ķ����������ɵý⣮
��2��������Ŀ��Ϣ�����ԭ�������Ա�����ȡֵ��Χ��Ϊ�������ĺ���ֵ�ķ�Χ��
��3�����ݷ������Ķ���ֱ������С��ķ����������ɵý⣮
����⣺��1����y=-2x+3�ã�x=
��
���ԣ�����y=-2x+3�ķ�������y=
��
��2������y=
���Ա�����ȡֵ��Χ��
x+1��0��
���x��-1��
���ԣ�����y=
�ķ������ĺ���ֵ��ȡֵ��ΧΪy��-1��
��3����y=x�ķ�����Ϊy=x��
��y=x+1�ķ�����Ϊy=x-1��
��y=-x+1�ķ�����Ϊy=1-x��
��y=
�ķ�����Ϊy=
��
��y=
��x��1���ķ�����Ϊy=
��
���ԣ������������������Т٢ܢݣ�
�ʴ�Ϊ����2��B����3���٢ܢݣ�
| 3-y |
| 2 |
���ԣ�����y=-2x+3�ķ�������y=
| 3-x |
| 2 |
��2������y=
| x-2 |
| x+1 |
x+1��0��
���x��-1��
���ԣ�����y=
| x-2 |
| x+1 |
��3����y=x�ķ�����Ϊy=x��
��y=x+1�ķ�����Ϊy=x-1��
��y=-x+1�ķ�����Ϊy=1-x��
��y=
| 1 |
| x |
| 1 |
| x |
��y=
| x+1 |
| x-1 |
| x+1 |
| x-1 |
���ԣ������������������Т٢ܢݣ�
�ʴ�Ϊ����2��B����3���٢ܢݣ�
���������⿼���˺�����ϵʽ�������Ա�����ȡֵ��Χ��������Ŀ��Ϣ�����ⷴ�����Ķ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
�����Ŀ
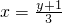 ������ԭ����y=3x-1�ķ�������
������ԭ����y=3x-1�ķ�������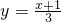
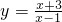 ��x��1��
��x��1��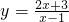 ���ɵ�
���ɵ�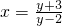 ������ԭ����
������ԭ����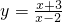 ��x��2��
��x��2�� �ķ������ĺ���ֵ��ȡֵ��ΧΪ______
�ķ������ĺ���ֵ��ȡֵ��ΧΪ______ ��
��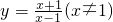 ��
��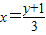 ������ԭ����y=3x-1�ķ�������
������ԭ����y=3x-1�ķ�������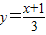
 ��x��1��
��x��1�� ���ɵ�
���ɵ� ������ԭ����
������ԭ����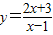 �ķ�������
�ķ�������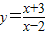 ��x��2��
��x��2�� �ķ������ĺ���ֵ��ȡֵ��ΧΪ______
�ķ������ĺ���ֵ��ȡֵ��ΧΪ______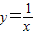 ��
�� ��
��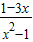 ��ʾ�ɲ��ַ�ʽ��
��ʾ�ɲ��ַ�ʽ�� ��
��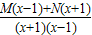 =
= ��
�� ���
���
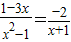 +
+
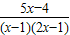 ��ʾ�ɲ��ַ�ʽ��
��ʾ�ɲ��ַ�ʽ��