Question

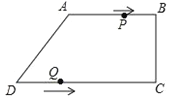
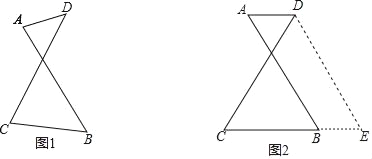
【题目】如图1有两条长度相等的相交线段AB、CD，它们相交的锐角中有一个角为60°，为了探究AD、CB与CD（或AB）之间的关系，小亮进行了如下尝试：

（1）在其他条件不变的情况下使得AD∥BC，如图2，将线段AB沿AD方向平移AD的长度，得到线段DE，然后联结BE，进而利用所学知识得到AD、CB与CD（或AB）之间的关系：　 　；（直接写出结果）

（2）根据小亮的经验，请对图1的情况（AD与CB不平行）进行尝试，写出AD、CB与CD（或AB）之间的关系，并进行证明；

（3）综合（1）、（2）的证明结果，请写出完整的结论：　 　．

Answer 1

【答案】AD+CB=AB

【解析】

(1)、根据图形得出线段之间的关系；(2)、将线段AB沿AD方向平移AD的长度，得到线段DE,根据平行四边形的性质、等边三角形的性质以及三角形三边之间的关系得出答案；(3)、根据两个结论得出答案即可．

（1）AD+CB=AB

（2）补全图形正确， 结论：

理由：如图：将线段AB沿AD方向平移AD的长度，得到线段DE,

联结BE、CE，且可得且，∴四边形A、B、E、D是平行四边形，

∴， ∵， ∴， ∵,，

∴是等边三角形∴，由于AD与CB不平行，所以C、B、E构成三角形，

∴ ， ∴；

（3）