Question

如图，一只蜘蛛在一块长方体木块的一个顶点A处，一只苍蝇在这个长方体的对角顶点G处，若AB=3cm，BC=5cm，BF=6cm，问蜘蛛要沿着怎样的路线爬行，才能最快抓到苍蝇？这时蜘蛛走过的路程是多少厘米？

Answer 1

分析：本题先把长方体展开，根据两点之间线段最短的性质，得出最短的路线是AG，然后求出展开后的线段AC、CG的长，再根据勾股定理求出AG即可．

解答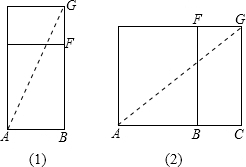：解：（1）如图（2）当蚂蚁从A出发先到BF上再到点G时
∵AB=3cm，BC=5cm
∴AC=AB+BC=3+5=8cm
∵BF=6cm，
∴CG=BF=6cm
在Rt△ABG中
AG=

AC2+CG2

=

82+62

=10cm

（2）如图（1）当蚂蚁从A出发先到EF上再到点G时
∵BC=5cm，
∴FG=BC=5cm，
∴BG=5+6=11cm
在Rt△ABG中
AG=

AB2+BG2

=

32+112

=

130

，∵

130

＞10

∴第一种方案最近，这时蜘蛛走过的路程是10cm．

点评：本题考查了两点之间线段最短的性质，以及对勾股定理的应用．