题目内容
 如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面五个结论:
如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面五个结论:①DE=1;②△CDE∽△CAB;③△CDE的面积与四边形ABED的面积之比为1:3;④梯形ABED的中位线长为
| 3 |
| 2 |
其中正确的有( )
分析:根据三角形中位线定理可得DE=
AB,DE∥AB,进而可得①②的正误;再根据相似三角形的面积之比等于对应边之比的平方可判断出③的正误;再根据梯形的中位线定理可计算出④的正误,然后再证明△DEG∽△BAG,再根据相似三角形的性质可判断出⑤.
| 1 |
| 2 |
解答:解:∵DE是△ACB的中位线,
∴DE=
AB,DE∥AB,
∵等边三角形ABC的边长为2,
∴AB=2,
∴DE=1,
故①正确;
∵DE∥AB,
∴△CDE∽△CAB,
故②正确;
∵△CDE∽△CAB,
∴
=
,
∴
=
,
∴△CDE的面积与四边形ABED的面积之比为1:3,
故③正确;
∵DE=1,AB=2,
∴
(AB+DE)=
,
故④正确;
∵DE∥AB,
∴△DEG∽△BAG,
∴
=
=
,
故⑤正确;
故选:D.
∴DE=
| 1 |
| 2 |

∵等边三角形ABC的边长为2,
∴AB=2,
∴DE=1,
故①正确;
∵DE∥AB,
∴△CDE∽△CAB,
故②正确;
∵△CDE∽△CAB,
∴
| DE |
| AB |
| 1 |
| 2 |
∴
| S△CDE |
| S△CAB |
| 1 |
| 4 |
∴△CDE的面积与四边形ABED的面积之比为1:3,
故③正确;
∵DE=1,AB=2,
∴
| 1 |
| 2 |
| 3 |
| 2 |
故④正确;
∵DE∥AB,
∴△DEG∽△BAG,
∴
| DG |
| BG |
| DE |
| AB |
| 1 |
| 2 |
故⑤正确;
故选:D.
点评:此题主要考查了相似三角形的判定与性质,以及三角形和梯形的中位线定理,关键是掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
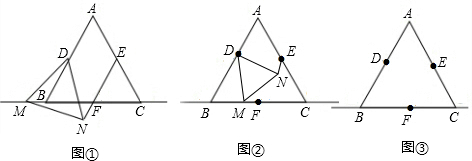
 23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.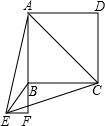 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F. 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想. 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动