题目内容
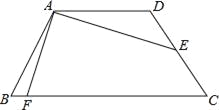
【题目】如图，已知四边形ABCD为等腰梯形，AD∥BC，AB=CD，AD=
，E为CD中点，连接AE，且AE=2
，∠DAE=30°，作AE⊥AF交BC于F，则BF=（ ）
A. 1 B. 3﹣ C. 
﹣1 D. 4﹣2
【答案】D
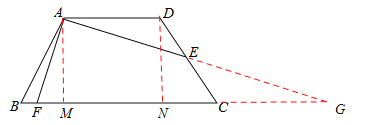
【解析】试题分析：如答图，延长AE交BC的延长线于G，
∵E为CD中点，∴CE=DE．
∵AD∥BC，∴∠DAE=∠G=30°．
∵在△ADE和△GCE中，∠DAE=∠G，∠AED=∠GEC，CE=DE，
∴△ADE≌△GCE（AAS）．∴CG=AD=
，AE=EG=2
．∴AG=AE+EG=2+2=4．
∵AE⊥AF，∴AF=AGtan30°=
，GF=AG÷cos30°=
．
过点A作AM⊥BC于M，过点D作DN⊥BC于N，则MN=AD=，
∵四边形ABCD为等腰梯形，∴BM=CN．
∵MG=AGcos30°=
，∴CN=MG﹣MN﹣CG=6﹣﹣=6﹣2．
∵AF⊥AE，AM⊥BC，∴∠FAM=∠G=30°．∴FM=AFsin30°=
．
∴BF=BM﹣MF=6﹣2﹣2=4﹣2．
故选D．
练习册系列答案
相关题目
