Question

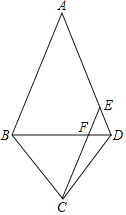
【题目】如图，在四边形ABCD中，AB＝AD，BC＝DC，点E为AD边上一点，连接BD、CE，CE与BD交于点F，且CE∥AB，若AB＝8，CE＝6，若△FCD的面积为2，则四边形ABCD的面积为_____．

Answer 1

【答案】24

【解析】

连接AC，证出AC垂直平分BD，由等腰三角形的性质得出∠ABD＝∠ADB，∠BAC＝∠DAC，由平行线的性质得出∠BAC＝∠ACE，∠ABD＝∠EFD，得出∠DAC＝∠ACE，∠ADB＝∠EFD，证出AE＝CE＝6，EF＝DE＝AD﹣AE＝2，得出CF＝CE﹣EF＝4＝2EF，得出△DEF的面积＝△FCD的面积＝，由平行线证明△EFD∽△ABD，得出＝，＝＝，求出S△ABD＝16S△EFD＝16，S△BCD＝4S△FCD＝8，即可得出答案．

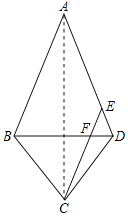
解：∵连接AC，如图所示：∵AB＝AD＝8，BC＝DC，

∴AC垂直平分BD，∠ABD＝∠ADB，

∴∠BAC＝∠DAC，

∵CE∥AB，

∴∠BAC＝∠ACE，∠ABD＝∠EFD，

∴∠DAC＝∠ACE，∠ADB＝∠EFD，

∴AE＝CE＝6，EF＝DE＝AD﹣AE＝2，

∴CF＝CE﹣EF＝4＝2EF，

∵△FCD的面积为2，

∴△DEF的面积＝△FCD的面积＝，

∵CE∥AB，

∴△EFD∽△ABD，且＝＝＝，

∴＝（）2＝，＝＝，

∴S△ABD＝16S△EFD＝16，S△BCD＝4S△FCD＝8，

∴四边形ABCD的面积＝△ABD的面积+△BCD的面积＝24；

故答案为：24．