题目内容
(人教版)已知平面直角坐标系中,B(-3,0),A为y轴正半轴上一动点,半径为| 5 |
| 2 |
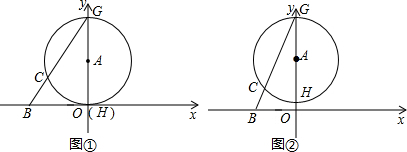
(1)如图①,当⊙A与x轴相切时,求直线BG的解析式;
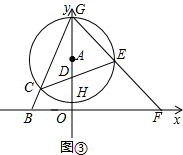
(2)如图②,若CG=2BC,求OA的长;
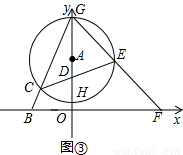
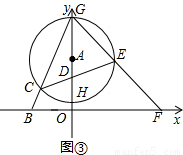
(3)如图③,D为半径AH上一点,且AD=1,过点D作⊙A的弦CE,连接GE并延长交x轴于点F,当⊙A与x轴相离时,给出下列结论:①
| OG2 |
| OF |
分析:(1)根据题意应先求出G点的坐标,再将B、G两点的坐标代入一次函数关系式y=kx+b中;
(2)由题意需过点C作CM⊥GH于点M,再利用比例线段求解;
(3)需连接CH、EH,作DN⊥EG于点N,再求
的值.
(2)由题意需过点C作CM⊥GH于点M,再利用比例线段求解;
(3)需连接CH、EH,作DN⊥EG于点N,再求
| OG2 |
| OF |
解答:解:(1)⊙A与x轴相切,OA=
,G(0,5).
设直线BG的解析式为:y=kx+b,将B、G两点的坐标代入一次函数关系式y=kx+b中,
,
解得:
得出直线BG的解析式为:y=
+5,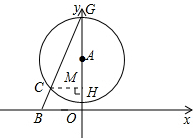
y=
+5.
(2)
过点C作CM⊥GH于点M,则CM∥BO,
∴△GCM∽△GBO,
∴
=
,
∵CG=2BC,B0=3,
∴
=
,
∴CM=2.
设GM=x,则MH=5-x,
∴x(5-x)=22,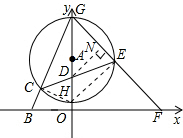
解得:xl=1,x2=4,
∴MG=1或MG=4.
GO=6或GO=
,
当GO=
<
,
则A点在y轴的负半轴,不合题意,故舍.
∴GO=6.∴OA=GO-AG=
.
(3)
的值不变,其值为7.
证明:连接CH、EH,作DN⊥EG于点N,则DN∥HE.
OG=OB•
①,
同理OG=FO•
②,
=0B•
=7,
故
的值不变,其值为7.
| 5 |
| 2 |
设直线BG的解析式为:y=kx+b,将B、G两点的坐标代入一次函数关系式y=kx+b中,
|
解得:
|
得出直线BG的解析式为:y=
| 5x |
| 3 |

y=
| 5x |
| 3 |
(2)
过点C作CM⊥GH于点M,则CM∥BO,
∴△GCM∽△GBO,
∴
| CG |
| BC |
| CM |
| BO |
∵CG=2BC,B0=3,
∴
| CM |
| 3 |
| 2 |
| 3 |
∴CM=2.
设GM=x,则MH=5-x,
∴x(5-x)=22,

解得:xl=1,x2=4,
∴MG=1或MG=4.
GO=6或GO=
| 3 |
| 2 |
当GO=
| 3 |
| 2 |
| 5 |
| 2 |
则A点在y轴的负半轴,不合题意,故舍.
∴GO=6.∴OA=GO-AG=
| 7 |
| 2 |
(3)
| OG2 |
| OF |
证明:连接CH、EH,作DN⊥EG于点N,则DN∥HE.
OG=OB•
| DN |
| NE |
同理OG=FO•
| GN |
| DN |
| OG2 |
| OF |
| GN |
| NE |
故
| OG2 |
| OF |
点评:此题作为压轴题,综合考查函数、方程与圆的切线,三角形相似的判定与性质等知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.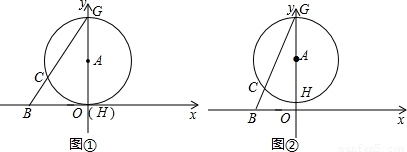
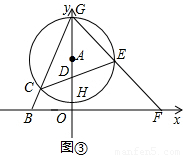
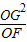 的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值. 的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.

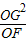 的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值. 的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.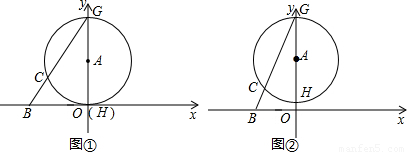
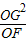 的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值. 的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.
的⊙A交y轴于点G、H(点G在点H的上方),连接BG交⊙A于点C.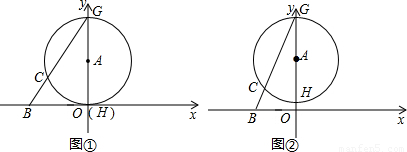
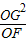 的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变;②OG•OF的值不变.其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.