题目内容
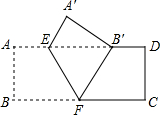（2013•南充）如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是（ ）分析：连接BE，根据矩形的对边平行可得AD∥BC，根据两直线平行，同旁内角互补可得∠AEF=120°，两直线平行，内错角相等可得∠DEF=60°，再根据翻折变换的性质求出∠BEF=∠DEF，然后求出∠AEB=60°，再解直角三角形求出AB，然后根据矩形的面积公式列式计算即可得解．
解答：
解：如图，连接BE，
在矩形ABCD中，AD∥BC，
∴∠AEF=180°-∠EFB=180°-60°=120°，
∠DEF=∠EFB=60°，
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处，
∴∠BEF=∠DEF=60°，
∴∠AEB=∠AEF-∠BEF=120°-60°=60°，
在Rt△ABE中，AB=AE•tan∠AEB=2tan60°=2
，
∵AE=2，DE=6，
∴AD=AE+DE=2+6=8，
∴矩形ABCD的面积=AB•AD=2
×8=16
．
故选D．
解：如图，连接BE，在矩形ABCD中，AD∥BC，
∴∠AEF=180°-∠EFB=180°-60°=120°，
∠DEF=∠EFB=60°，
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处，
∴∠BEF=∠DEF=60°，
∴∠AEB=∠AEF-∠BEF=120°-60°=60°，
在Rt△ABE中，AB=AE•tan∠AEB=2tan60°=2
| 3 |
∵AE=2，DE=6，
∴AD=AE+DE=2+6=8，
∴矩形ABCD的面积=AB•AD=2
| 3 |
| 3 |
故选D．
点评：本题考查了矩形的性质，翻折变换的性质，两直线平行，同旁内角互补，两直线平行，内错角相等的性质，解直角三角形，作辅助线构造直角三角形并熟记性质是解题的关键．
练习册系列答案
相关题目
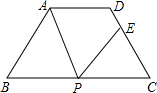（2013•南充）如图，等腰梯形ABCD中，AD∥BC，AD=3，BC=7，∠B=60°，P为BC边上一点（不与B，C重合），过点P作∠APE=∠B，PE交CD于E．
（2013•南充）如图，正方形ABCD的边长为2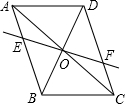
（2013•南充）如图，在平行四边形ABCD中，对角线AC，BD交于点O，经过点O的直线交AB于E，交CD于F．
（2013•南充）如图，二次函数y=x2+bx-3b+3的图象与x轴交于A，B两点（点A在点B的左边），交y轴于点C，且经过点（b-2，2b2-5b-1）．