题目内容
【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .
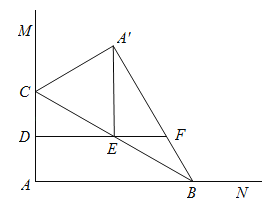
【答案】![]() 或
或![]()
【解析】
当△![]() 为直角三角形时,存在两种情况:
为直角三角形时,存在两种情况:
①当![]() 时,如图1,根据对称的性质和平行线可得:
时,如图1,根据对称的性质和平行线可得:![]() ,根据直角三角形斜边中线的性质得:
,根据直角三角形斜边中线的性质得:![]() ,最后利用勾股定理可得
,最后利用勾股定理可得![]() 的长;
的长;
②当![]() 时,如图2,证明
时,如图2,证明![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() .
.
解:当△![]() 为直角三角形时,存在两种情况:
为直角三角形时,存在两种情况:
①当![]() 时,如图1,
时,如图1,
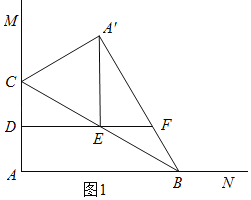
![]() △
△![]() 与
与![]() 关于
关于![]() 所在直线对称,
所在直线对称,
![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
![]() 、
、![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() △
△![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,
的中点,
![]() ,
,
由勾股定理得:![]() ,
,
![]() ;
;
②当![]() 时,如图2,
时,如图2,
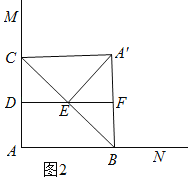
![]() ,
,
![]() ,
,
![]() △
△![]() 与
与![]() 关于
关于![]() 所在直线对称,
所在直线对称,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ;
;
综上所述,![]() 的长为
的长为![]() 或4;
或4;
故答案为:![]() 或4;
或4;

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目