Question

国强同学喜欢用黑色棋子摆放在正多边形的边上来研究数的规律．请你观察下面表格中棋子的摆放规律，并回答下面问题：

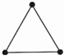
三角形				…	第n个 三角形
棋子个数	3	6	9	…	P
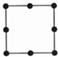
正方形				…	第n个 正方形
棋子个数	4	8	12	…	Q
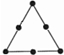
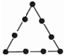
正多边形					第n个 正多边形
棋子个数	3	8	15	24	M

（1）通过观察、归纳发现可以分别用含字母n（n≥1的整数）的代数式表示P、Q、M．
则P=______，Q=______，M=______．
（2）下列数中既是三角形中的棋子数又是正方形中的棋子数的是______．
A.2013　　B.2014　 C.2015　　D.2016．

Answer 1

解：（1）P第一个图形有3个棋子，第二个图形有6个棋子，第三个图形有9个棋子，…，第n个图形有3n个棋子；
Q第一个图形有4个棋子，第二个图形有8个棋子，第三个图形有12个棋子，…，第n个图形有4n个棋子，
M第一个图形有3个棋子，第二个图形有8个棋子，8=（2+1）×（2+2）-（2+2）=4×2，
第三个图形有15个棋子，15=（3+1）×（3+2）-（3+2）=5×3，
第四个图形有24个棋子，24=（4+1）×（4+2）-（4+2），
…，
第n个图形有n（n+2）个棋子；

（2）∵三角形中的棋子数符合3n，正方形中的棋子数符合4n，
∴既是三角形中的棋子数又是正方形中的棋子数是12的倍数，
∵2013、2014、2015、2016四个数中只有2016是12的倍数，
∴既是三角形中的棋子数又是正方形中的棋子数的是2016．
故答案为：（1）3n，4n，n（n+2）；（2）D．
分析：（1）根据P、Q的棋子数的变化特征写出即可，M的棋子数等于边数乘以每条边上的棋子数，根据顶点处的棋子是公用的棋子，再减去顶点的个数即可得解；
（2）根据P、Q的表达式找出是12的倍数的数值即可．
点评：本题是对图形变化规律的考查，难点在于观察出多边形时边的表示与边上的棋子的个数与多边形所在图形序数的关系．