题目内容
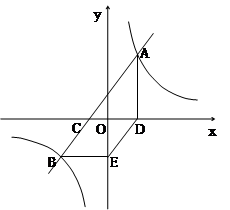
 如图,已知直线AB的解析式y=mx+n,它与x轴交于点C,与双曲线y=
如图,已知直线AB的解析式y=mx+n,它与x轴交于点C,与双曲线y=| k |
| x |
| 20 |
| 3 |
(1)求反比例函数的解析式及直线AB的解析式;
(2)根据函数图象可知,当mx+n-
| k |
| x |
-5<x<0或x>3
-5<x<0或x>3
;(3)判断四边形CBED的形状,并说明理由.
分析:(1)利用双曲线y=
过A(3,
),直接求出k即可,利用B的值代入反比例函数解析式得出a,进而求出一次函数的解析式;
(2)利用函数图象得出一次函数大于反比例函数时x的取值范围;
(3)利用CD=5,BE=5,且BE∥CD,得出四边形CBED是平行四边形,再利用ED=CD,得出平行四边形CBED是菱形.
| k |
| x |
| 20 |
| 3 |
(2)利用函数图象得出一次函数大于反比例函数时x的取值范围;
(3)利用CD=5,BE=5,且BE∥CD,得出四边形CBED是平行四边形,再利用ED=CD,得出平行四边形CBED是菱形.
解答:解:(1)∵双曲线y=
过A(3,
),
∴k=20.
把B(-5,a)代入y=
,得a=-4.
∴点B的坐标是(-5,-4).
将 A(3,
)、B(-5,-4)代入y=mx+n,得,
,
解得:m=
,n=
.
∴直线AB的解析式为:y=
x+
.
(2)当mx+n-
>0时,
即y=mx+n大于反比例函数y=-
时,x的取值范围,
利用图象可得:-5<x<0或x>3时,mx+n-
>0;
(3)四边形CBED是菱形.理由如下:
点D的坐标是(3,0),点C的坐标是(-2,0).
∵BE∥x轴,
∴点E的坐标是(0,-4).
而CD=5,BE=5,且BE∥CD.
∴四边形CBED是平行四边形.
在Rt△OED中,ED2=OE2+OD2,
∴ED=
=5,
∴ED=CD.
∴平行四边形CBED是菱形.
| k |
| x |
| 20 |
| 3 |
∴k=20.
把B(-5,a)代入y=
| 20 |
| x |
∴点B的坐标是(-5,-4).
将 A(3,
| 20 |
| 3 |
|
解得:m=
| 4 |
| 3 |
| 8 |
| 3 |
∴直线AB的解析式为:y=
| 4 |
| 3 |
| 8 |
| 3 |
(2)当mx+n-
| k |
| x |
即y=mx+n大于反比例函数y=-
| k |
| x |
利用图象可得:-5<x<0或x>3时,mx+n-
| k |
| x |
(3)四边形CBED是菱形.理由如下:
点D的坐标是(3,0),点C的坐标是(-2,0).
∵BE∥x轴,
∴点E的坐标是(0,-4).
而CD=5,BE=5,且BE∥CD.
∴四边形CBED是平行四边形.
在Rt△OED中,ED2=OE2+OD2,
∴ED=
| 32+42 |
∴ED=CD.
∴平行四边形CBED是菱形.
点评:此题主要考查了待定系数法求一次函数与反比例的解析式以及菱形的判定与性质等知识,利用数形结合比较得出函数值大小以及结合菱形判定得出是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,已知直线AB的解析式是y=-2x+4,直线AC的解析式是y=x+4,过C点作CE⊥AB,垂足为E,交y轴于点D.求点D的坐标.
如图,已知直线AB的解析式是y=-2x+4,直线AC的解析式是y=x+4,过C点作CE⊥AB,垂足为E,交y轴于点D.求点D的坐标.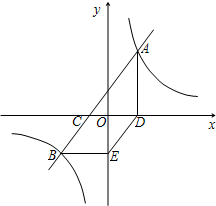 如图,已知直线AB的解析式y=mx+n,它与x轴交于点C,与双曲线
如图,已知直线AB的解析式y=mx+n,它与x轴交于点C,与双曲线 交于A(3,
交于A(3, )、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E. >0时,x的取值范围是______;
>0时,x的取值范围是______; )、B(-5,
)、B(-5, 轴且与
轴且与 >0时,x的取值范围是 ;
>0时,x的取值范围是 ;
 轴交于点C,与双曲线
轴交于点C,与双曲线 交于A(3,
交于A(3,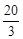 )、B(-5,
)、B(-5,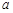 )两点.AD⊥
)两点.AD⊥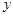 轴交于点E.
轴交于点E. >0时,x的取值范围是 ;
>0时,x的取值范围是 ;