题目内容
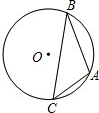 如图,点A、B、C是⊙O上的点,且AB=4,∠ACB=45°,则⊙O的半径等于________.
如图,点A、B、C是⊙O上的点,且AB=4,∠ACB=45°,则⊙O的半径等于________.
2
分析:过A点作直径AD,连BD,根据圆周角定理及其推论得到∠DBA=90°,∠D=∠C=45°,则△ABD为等腰直角三角形,根据等腰直角三角形的斜边是直角边的 倍得到AD=
倍得到AD= AB=4
AB=4 ,即可得到半径OA.
,即可得到半径OA.
解答: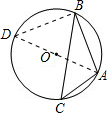 解:过A点作直径AD,连BD,如图,
解:过A点作直径AD,连BD,如图,
∴∠DBA=90°,∠D=∠C=45°,
∴△ABD为等腰直角三角形,
而AB=4,
∴AD= AB=4
AB=4 ,
,
∴OA=2 .
.
故答案为:2 .
.
点评:本题考查了圆周角定理及其推论:同弧所对的圆周角相等;直径所对的圆周角为直角.也考查了等腰直角三角形三边的关系.

分析:过A点作直径AD,连BD,根据圆周角定理及其推论得到∠DBA=90°,∠D=∠C=45°,则△ABD为等腰直角三角形,根据等腰直角三角形的斜边是直角边的
 倍得到AD=
倍得到AD= AB=4
AB=4 ,即可得到半径OA.
,即可得到半径OA.解答:
 解:过A点作直径AD,连BD,如图,
解:过A点作直径AD,连BD,如图,∴∠DBA=90°,∠D=∠C=45°,
∴△ABD为等腰直角三角形,
而AB=4,
∴AD=
 AB=4
AB=4 ,
,∴OA=2
 .
.故答案为:2
 .
.点评:本题考查了圆周角定理及其推论:同弧所对的圆周角相等;直径所对的圆周角为直角.也考查了等腰直角三角形三边的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 8、如图,点A,B,C是⊙O上的三点,∠BAC=40°,则∠OBC的度数是( )
8、如图,点A,B,C是⊙O上的三点,∠BAC=40°,则∠OBC的度数是( ) 如图,点A、B、C是⊙O上的三点,若∠BOC=50°,则∠A的度数为
如图,点A、B、C是⊙O上的三点,若∠BOC=50°,则∠A的度数为
 如图,点A、B、C是⊙O上的三点,∠BAC=40°,则∠BOC的度数是( )
如图,点A、B、C是⊙O上的三点,∠BAC=40°,则∠BOC的度数是( ) 如图,点A、B、C是圆O上的三点,OB⊥AC,∠BAC=40°,则∠OCA=( )
如图,点A、B、C是圆O上的三点,OB⊥AC,∠BAC=40°,则∠OCA=( )