题目内容
如图,抛物线 的顶点为Q,与
的顶点为Q,与 轴交于A(-1,0)、B(5, 0)两点,与
轴交于A(-1,0)、B(5, 0)两点,与 轴交于C点.
轴交于C点.

(1)直接写出抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线的对称轴上求一点 ,使得△
,使得△ 的周长最小.请在图中画出点
的周长最小.请在图中画出点 的位置,并求点
的位置,并求点 的坐标.
的坐标.
【答案】
见解析
【解析】
试题分析:(1) 抛物线 与
与 轴交于A(-1,0)、B(5, 0)两点,根据一元二次方程与二次函数的关系可得
轴交于A(-1,0)、B(5, 0)两点,根据一元二次方程与二次函数的关系可得 是
是 的两根,根据根与系数的关系得b=4,c=5所以
的两根,根据根与系数的关系得b=4,c=5所以 ,配方得出
,配方得出 写出顶点Q的坐标Q(2,9).
写出顶点Q的坐标Q(2,9).
(2)如图,连接BC,交对称轴于点P,连接AP、AC.因为AC长为定值,所以,要使△PAC的周长最小,只需PA+PC最小. 而点A关于对称轴 =1的对称点是点B(5,0),抛物线
=1的对称点是点B(5,0),抛物线 与y轴交点C的坐标为(0,5).
与y轴交点C的坐标为(0,5).

∴由几何知识可知,PA+PC=PB+PC为最小. 不妨设直线BC的解析式为y=k +5,
+5,
将B(5,0)代入5k+5=0,得k=-1, =-
=- +5,与对称轴的交点就是P,所以
+5,与对称轴的交点就是P,所以 =2时,y=3 ,即点P的坐标为(2,3).
=2时,y=3 ,即点P的坐标为(2,3).
试题解析:(1)  ,
,
∴Q(2 ,9).
(2)如解析图,连接BC,交对称轴于点P,连接AP、AC.
∵AC长为定值,∴要使△PAC的周长最小,只需PA+PC最小.
∵点A关于对称轴 =1的对称点是点B(5,0),抛物线
=1的对称点是点B(5,0),抛物线 与y轴交点C的坐标为(0,5).
与y轴交点C的坐标为(0,5).
∴由几何知识可知,PA+PC=PB+PC为最小.
设直线BC的解析式为y=k +5,
+5,
将B(5,0)代入5k+5=0,得k=-1,
∴ =-
=- +5,
+5,
∴当 =2时,y=3 ,∴点P的坐标为(2,3).
=2时,y=3 ,∴点P的坐标为(2,3).
考点:1.抛物线顶点坐标.2. 抛物线的解析式.3. 物线的对称轴上求一点,使三角形的周长最小

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 点.
点. 21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).
21、如图,抛物线的顶点为A(1,-4),且过点B(3,0). (2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
(2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 (2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.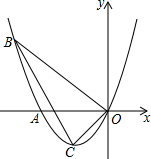 (2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.