题目内容
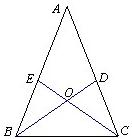 19、在△ABC中,D,E分别是AC,AB上的点,BD与CE交于O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.请你从上述四个条件中选出两个条件,然后利用这两个条件证明△ABC是等腰三角形.(选出的条件用序号表示)
19、在△ABC中,D,E分别是AC,AB上的点,BD与CE交于O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.请你从上述四个条件中选出两个条件,然后利用这两个条件证明△ABC是等腰三角形.(选出的条件用序号表示)分析:此题是开放性试题,解答时根据题中已知条件,结合等腰三角形的判定方法来选择.
解答:解:可以选择①③;①④;②③;②④.
选①③证明;
∵∠EBO=∠DCO,BE=CD,∠EOB=∠DOC,
∴△EOB≌△DOC.
∴OB=OC.
∴∠OBC=∠OCB.
∵∠ABC=∠EBO+∠OBC,∠ACB=∠DCO+∠OCB,
∴∠ABC=∠ACB.
∴△ABC是等腰三角形.
选①③证明;
∵∠EBO=∠DCO,BE=CD,∠EOB=∠DOC,
∴△EOB≌△DOC.
∴OB=OC.
∴∠OBC=∠OCB.
∵∠ABC=∠EBO+∠OBC,∠ACB=∠DCO+∠OCB,
∴∠ABC=∠ACB.
∴△ABC是等腰三角形.
点评:本题考查了等腰三角形的判定及全等三角形的判定及性质;选择条件时要注意选择相对比较简单的,比较容易证明的,经常要结合三角形全等进行证明.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于