题目内容
 如图,在⊙O中,OE为半径,点D为OE的中点,AB是过点D且垂直于OE的弦,点C是优弧ACB上任意一点,则∠ACB度数是
如图,在⊙O中,OE为半径,点D为OE的中点,AB是过点D且垂直于OE的弦,点C是优弧ACB上任意一点,则∠ACB度数是
- A.30°
- B.50°
- C.60°
- D.无法确定
C
分析:连接OA,OB,根据垂径定理和圆周角定理求解.
解答: 解:连接OA,OB,
解:连接OA,OB,
根据题意,得OD= OA,
OA,
则∠AOD=60°,∠AOB=120°.
根据圆周角定理,得:
∠ACB=60°.
故选C.
点评:此题要能够根据直角三角形的三边关系求得角的度数.然后根据垂径定理以及圆周角定理.
分析:连接OA,OB,根据垂径定理和圆周角定理求解.
解答:
 解:连接OA,OB,
解:连接OA,OB,根据题意,得OD=
 OA,
OA,则∠AOD=60°,∠AOB=120°.
根据圆周角定理,得:
∠ACB=60°.
故选C.
点评:此题要能够根据直角三角形的三边关系求得角的度数.然后根据垂径定理以及圆周角定理.

练习册系列答案
相关题目
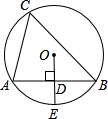 如图,在⊙O中,OE为半径,点D为OE的中点,AB是过点D且垂直于OE的弦,点C是优弧ACB上任意一点,则∠ACB度数是( )
如图,在⊙O中,OE为半径,点D为OE的中点,AB是过点D且垂直于OE的弦,点C是优弧ACB上任意一点,则∠ACB度数是( )| A、30° | B、50° | C、60° | D、无法确定 |
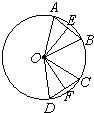 16、如图,在⊙O中,OE⊥AB于点E,OF⊥CD于点F,要使OE=OF,则需添加条件是
16、如图,在⊙O中,OE⊥AB于点E,OF⊥CD于点F,要使OE=OF,则需添加条件是