题目内容
如图，以点P为圆心，以
为半径的圆弧与x轴交于A，B两点，点A的坐标为（2，0），点B的坐标为（6，0），则圆心P的坐标为
- A.（4，
） - B.（4，2）
- C.（4，4）
- D.（2，
）
C
分析：过点P作PC⊥AB于点C，利用垂径定理以及结合点A和点B的坐标即可得出点C的坐标，即可得出AC的长度，从而可得出PC的长度，且点P位于第一象限，即可得出P的坐标．
解答：
解：过点P作PC⊥AB于点C；
即点C为AB的中点，
又点A的坐标为（2，0），点B的坐标为（6，0），
故点C（4，0）
在Rt△PAC中，PA=，AC=2，
即有PC=4，
即P（4，4）．
故选C．
点评：本题主要考查垂径定理的应用和解直角三角形的应用，要求学生能够准确作出辅助线，灵活运用所学知识．
分析：过点P作PC⊥AB于点C，利用垂径定理以及结合点A和点B的坐标即可得出点C的坐标，即可得出AC的长度，从而可得出PC的长度，且点P位于第一象限，即可得出P的坐标．
解答：
解：过点P作PC⊥AB于点C；即点C为AB的中点，
又点A的坐标为（2，0），点B的坐标为（6，0），
故点C（4，0）
在Rt△PAC中，PA=
，AC=2，即有PC=4，
即P（4，4）．
故选C．
点评：本题主要考查垂径定理的应用和解直角三角形的应用，要求学生能够准确作出辅助线，灵活运用所学知识．
练习册系列答案
相关题目
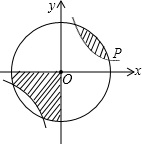如图，以点O为圆心的圆与反比例函数的图象相交，若其中一个交点P的坐标为（5，1），则图中两块阴影部分的面积和为
如图，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，且AB=4，OP=2，连接OA交小圆于点E，则扇形OEP的面积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
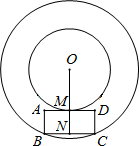26、如图，以点O为圆心的两个同心圆中，矩形ABCD的边BC为大圆的弦，边AD与小圆相切于点M，OM的延长线与BC相交于点N．
如图，以点O为圆心的两个同心圆，当大圆的弦AB与小圆相切时弦长AB=8，则这两个同心圆所形成的圆环的面积是
如图，以点P为圆心，半径为5的圆弧与x轴交于点A、B两点，点A、B坐标分别为（0，3）和（0，9），则点P的坐标为