题目内容
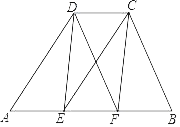
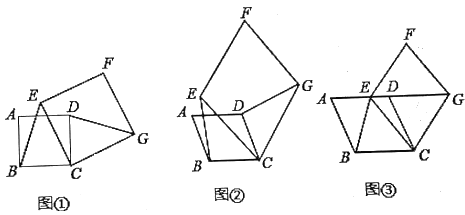
【题目】(1)(感知)如图①,四边形![]() 、
、![]() 均为正方形.
均为正方形.![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)(拓展)如图②,四边形![]() 、
、![]() 均为菱形,且
均为菱形,且![]() .请判断
.请判断![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
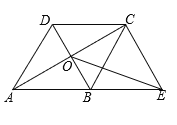
(3)(应用)如图③,四边形![]() 、
、![]() 均为菱形,点
均为菱形,点![]() 在边
在边![]() 上,点
上,点![]() 在
在![]() 延长线上.若
延长线上.若![]() ,
,![]() ,
,![]() 的面积为9,则菱形
的面积为9,则菱形![]() 的面积为_______.
的面积为_______.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)24.
;(3)24.
【解析】
(1)根据正方形的性质证明△BCE≌△DCG即可求解;
(2)根据菱形的性质证明△BCE≌△DCG即可求解;
(3)由AD∥BC,△BCE≌△DCG可得S△ABE+S△CDE=S△BEC=S△CDG=9,又AE=2ED,可求出△CDE的面积,继而求出答案.
解:(1) ∵四边形![]() 、
、![]() 均为正方形
均为正方形
∴BC=DC,EC=GC,
∵![]()
即![]() .
.
∴![]()
∴![]()
(2)∵四边形![]() 、四边形
、四边形![]() 均为菱形,
均为菱形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]()
即![]() .
.
∴![]() ,
,
∴![]() .
.
(3)∵四边形ABCD为菱形,∴AD∥BC,
∴△BCE≌△DCG可得S△ABE+S△CDE=S△BEC=S△CDG=9,又AE=2ED,
∴S△CDE=![]()
∴S△ECG=S△CDE+S△CDG=12,
∴S菱形CEFG=2S△ECG=24.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目