Question

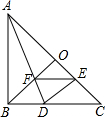如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．观察下列结论：
①tan∠DFE=2；
②若将△DEF沿EF折叠，则点D不一定落在AC上；
③2S_{四边形DFOE}=S_△ABD；
④图中有4对全等三角形；
⑤CD∥EF．
其中正确结论的有________（填序号）．

Answer 1

③、④、⑤
分析：根据折叠的知识，锐角正切值的定义，全等三角形的判定，面积的计算判断所给选项是否正确即可．
解答：①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；
②∵AB=CB，BO⊥AC，把△ABC折叠，
∴∠ABO=∠CBO=45°，∠FBD=∠DEF，
∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故②错误；
③连接CF，

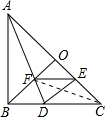
∵△AOF和△COF等底同高，
∴S_△AOF=S_△COF，
∵∠AEF=∠ACD=45°，
∴EF∥CD，故⑤正确；
∴S_△EFD=S_△EFC，
∴S_{四边形DFOE}=S_△COF，
∴S_{四边形DFOE}=S_△AOF，
又S_△ABD=S_△ADE=S_△AOF+S_{四边形DFOE}=2S_{四边形DFOE}，
故③正确；
④图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知）
∵OB⊥AC，∴∠AOB=∠COB=90°，
在Rt△AOB和Rt△COB中，
，
∴Rt△AOB≌Rt△COB（HL），
则全等三角形共有4对，故④正确．
正确的有③、④、⑤．
故答案为：③、④、⑤．
点评：本题综合考查了由折叠得到的相关问题；注意由对称也可得到一对三角形全等；用到的知识点为：三角形的中线把三角形分成面积相等的2部分；两条平行线间的距离相等．