题目内容
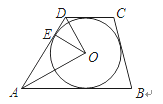
【题目】如图，在梯形ABCD中，AB∥CD，⊙O为内切圆，E为切点．
(1)求证：AO2=AEAD；
(2)若AO=4cm，AD=5cm，求⊙O的面积．
【答案】(1)证明见解析；(2)
π．
【解析】
（1）利用切线的性质以及切线长定理得出∠AOD=90°，进而得出△AOE∽△ADO，进而得出答案；
（2）利用三角形面积公式以及圆的面积公式求出即可．
(1)根据切线长定理可知：
∵∠OAE+∠ODA=
（∠BAD+∠ADC）=90°，
∴∠AOD=90°，
∵∠OAE=∠OAE，∠AOD=∠AEO=90°，
∴△AOE∽△ADO，
∴
即AO2=AEAD
(2)在Rt△AOD中，
OD=
=3，
∵S△AOD=×AD×EO=×AO×OD
即5×EO=4×3，
∴EO=
，
∵OE是⊙O的半径，
∴S圆O=πr2=π．
练习册系列答案
阅读快车系列答案
相关题目
