题目内容
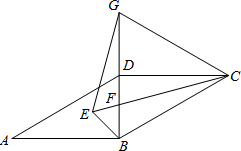 如图,在?ABCD中,对角线BD⊥AB,G为BD延长线上一点且△CBG为等边三角形,∠BCD、∠ABD的角平分线相交于点E,连接CE交BD于点F,连接GE.
如图,在?ABCD中,对角线BD⊥AB,G为BD延长线上一点且△CBG为等边三角形,∠BCD、∠ABD的角平分线相交于点E,连接CE交BD于点F,连接GE.
(1)若CG的长为8,求?ABCD的面积;
(2)求证:CE=BE+GE.
(1)解: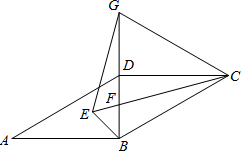 ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∵AB⊥DB,
∴CD⊥BD,
∵△BGC是等边三角形,
∴BG=BC=CG=8,
∴GD=DB= BG=4(三线合一定理),
BG=4(三线合一定理),
在Rt△GDC中,由勾股定理得:CD= =4
=4 ,
,
∴平行四边形ABCD的面积是CD×BD=4 ×4=16
×4=16 ;
;
(2)证明:∵△BCG为等边三角形,
∴∠GBC=∠BGC=∠GCB=60°,
∵BD⊥DC,
∴∠BCD=30°.
∵EC是∠BCD的平分线,
∴∠BCE=∠DCE=15°.
∵BE是∠ABD的平分线,∠ABD=90°,
∴∠EBD=45°,∠EBC=45°+60°=105°.
则∠BEC=180°-105°-15°=60°,
∴∠BEC=∠FBC,
∵∠BCF=∠BCE,
∴△CFB∽△CBE,
∴ =
= ,
,
∵∠GCE=60°-15°=45°=∠EBF,∠BFE=∠GFC,
∴△BFE∽△CFG,
∴ =
=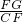 ,
,
∵∠EFG=∠BFC,
∴△EFG∽△BFC
∴∠GEF=∠CBF=60°,而∠BGC=60°,
∴△CGF∽△CEG,
∴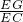 =
= ,
,
∴ +
+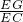 =
= +
+ ,
,
∵△BCG为等边三角形,
∴BC=CG=BG=BF+FG
∴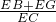 =1,
=1,
∴CE=BE+GE.
分析:(1)根据平行四边形性质推出CD⊥BD,根据等边三角形的性质得出GC=BC,推出BD=DQ,根据勾股定理求出DC,根据面积公式求出即可;
(2)证△CFB∽△CBE,推出 =
= ,证△BFE∽△CFG,推出
,证△BFE∽△CFG,推出 =
=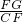 ,证△CGF∽△CEG,推出
,证△CGF∽△CEG,推出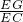 =
= ,得出
,得出 +
+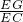 =
= +
+ ,根据BC=CG=BG=BF+FG推出
,根据BC=CG=BG=BF+FG推出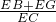 =1即可.
=1即可.
点评:本题考查了平行四边形性质,勾股定理,等腰三角形的性质,等边三角形的性质,三角形的内角和定理,相似三角形的性质和判定等知识点的综合运用,本题综合性比较强,难度偏大.
 ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,∴CD∥AB,
∵AB⊥DB,
∴CD⊥BD,
∵△BGC是等边三角形,
∴BG=BC=CG=8,
∴GD=DB=
 BG=4(三线合一定理),
BG=4(三线合一定理),在Rt△GDC中,由勾股定理得:CD=
 =4
=4 ,
,∴平行四边形ABCD的面积是CD×BD=4
 ×4=16
×4=16 ;
;(2)证明:∵△BCG为等边三角形,
∴∠GBC=∠BGC=∠GCB=60°,
∵BD⊥DC,
∴∠BCD=30°.
∵EC是∠BCD的平分线,
∴∠BCE=∠DCE=15°.
∵BE是∠ABD的平分线,∠ABD=90°,
∴∠EBD=45°,∠EBC=45°+60°=105°.
则∠BEC=180°-105°-15°=60°,
∴∠BEC=∠FBC,
∵∠BCF=∠BCE,
∴△CFB∽△CBE,
∴
 =
= ,
,∵∠GCE=60°-15°=45°=∠EBF,∠BFE=∠GFC,
∴△BFE∽△CFG,
∴
 =
=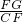 ,
,∵∠EFG=∠BFC,
∴△EFG∽△BFC
∴∠GEF=∠CBF=60°,而∠BGC=60°,
∴△CGF∽△CEG,
∴
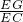 =
= ,
,∴
 +
+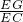 =
= +
+ ,
,∵△BCG为等边三角形,
∴BC=CG=BG=BF+FG
∴
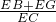 =1,
=1,∴CE=BE+GE.
分析:(1)根据平行四边形性质推出CD⊥BD,根据等边三角形的性质得出GC=BC,推出BD=DQ,根据勾股定理求出DC,根据面积公式求出即可;
(2)证△CFB∽△CBE,推出
 =
= ,证△BFE∽△CFG,推出
,证△BFE∽△CFG,推出 =
=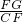 ,证△CGF∽△CEG,推出
,证△CGF∽△CEG,推出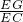 =
= ,得出
,得出 +
+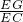 =
= +
+ ,根据BC=CG=BG=BF+FG推出
,根据BC=CG=BG=BF+FG推出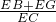 =1即可.
=1即可.点评:本题考查了平行四边形性质,勾股定理,等腰三角形的性质,等边三角形的性质,三角形的内角和定理,相似三角形的性质和判定等知识点的综合运用,本题综合性比较强,难度偏大.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=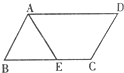 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.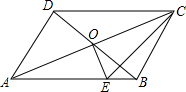 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是