Question

如图，平行四边形ABCD中，E是AB的中点，在直线AD上截取AF=2FD，连接EF，EF交AC于G．求AG：AC．

Answer 1

解：有两种情况：
第一种情况：F在线段AD上，如图1，
过点F作FH∥DC，交AC于点H，
∵AF=2FD，
∴在△ADC中，==2，且 ==，
∴AH=2HC…①，…②，
∵AE==…③，
又∵平行四边形ABCD，AB∥CD且AB=CD，
∴FH∥AB，
∴…④，
②③代入④得，
∴，
∴AH=AG+GH==2HC，
∴，
∵AC=AH+HC=3HC，
∴AG：AC=；

第二种情况：F在AD的延长线上，如图（2），
过点F作FH∥DC，交AC的延长线于点H，
∵AF=2FD
∴在△AFH中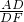，==且==，
∴AC=CH，FH=2CD，
∵AE==，
又∵FH∥AB，
∴===，
∴GH=4AG，
∴AH=AG+GH=5AG=2AC，
∴，
∴AG：AC=．
分析：本题分两种情况讨论：
（1）F在线段AD上，如图1，根据平行线分线段成比例定理，可得==2，且 ==，可得AH=2HC，FH=CD，AE==，则可得，代入整理，可得，，所以可得AH=2HC，，即可得出；
（2）F在AD的延长线上，如图2；在△AFH中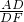，==且==，则AC=CH，FH=2CD，又由FH∥AB，可得===，即GH=4AG，所以AH=AG+GH=5AG=2AC，即可得出．
点评：本题主要考查了平分线分线段成比例定理和平行线四边形的性质，考查了学生对平行线分线段成比例定理的理解和综合应用能力．