题目内容
如图，△ABC是等腰直角三角形，DE过直角顶点A，∠D=∠E=90°，则下列结论正确的个数有
①CD=AE；②∠1=∠2；③∠3=∠4；④AD=BE．
- A.1个
- B.2个
- C.3个
- D.4个
B
分析：根据直角三角形的性质推出∠2=∠3，然后利用AAS证明△ABE和△CAD全等，根据全等三角形对应边相等，全等三角形对应角相等即可对各小题进行判断．
解答：∵∠D=90°，
∴∠1+∠3=90°，
∵△ABC是等腰直角三角形，A为直角顶点，
∴∠1+∠2=180°-90°=90°，AB=AC，
∴∠2=∠3，
在△ABE和△CAD中，
，
∴△ABE≌△CAD（AAS），
∴CD=AE，AD=BE，∠1=∠4，
故①小题正确，②小题错误，③小题错误，④小题正确，
所以结论正确的有①④共2个．
故选B．
点评：本题考查了全等三角形的判定与性质，等腰直角三角形直角边相等的性质，根据直角三角形的性质得到∠2=∠3是证明三角形全等的关键，也是解题的突破口．
分析：根据直角三角形的性质推出∠2=∠3，然后利用AAS证明△ABE和△CAD全等，根据全等三角形对应边相等，全等三角形对应角相等即可对各小题进行判断．
解答：∵∠D=90°，
∴∠1+∠3=90°，
∵△ABC是等腰直角三角形，A为直角顶点，
∴∠1+∠2=180°-90°=90°，AB=AC，
∴∠2=∠3，
在△ABE和△CAD中，
，∴△ABE≌△CAD（AAS），
∴CD=AE，AD=BE，∠1=∠4，
故①小题正确，②小题错误，③小题错误，④小题正确，
所以结论正确的有①④共2个．
故选B．
点评：本题考查了全等三角形的判定与性质，等腰直角三角形直角边相等的性质，根据直角三角形的性质得到∠2=∠3是证明三角形全等的关键，也是解题的突破口．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
如图，△ABC是等腰直角三角形，BC是斜边，点P是△ABC内一定点，延长BP至P′，将△ABP绕点A旋转后，与△ACP′重合，如果AP=
如图，△ABC是等腰直角三角形，∠ACB=90°，BC=AC，把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′，若AB=2，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是
（2012•资阳）如图，△ABC是等腰三角形，点D是底边BC上异于BC中点的一个点，∠ADE=∠DAC，DE=AC．运用这个图（不添加辅助线）可以说明下列哪一个命题是假命题？（ ）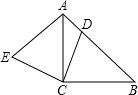
已知：如图，△ABC是等腰直角三角形，D为斜边AB上任意一点（不与A，B重合），连接CD，作EC⊥DC，且EC=DC，连接AE．