题目内容
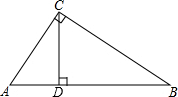△ABC中，∠BAC=90°，AD⊥BC于D，图中共有________对相似三角形．
3
分析：根据等角的余角相等可得：∠ACD=∠CBD，利用两角法可确定图中的相似三角形．
解答：∵∠ACD+∠DCB=90°，∠CBD+∠DCB=90°，
∴∠ACD=∠CBD，
又∵∠ADC=∠CDB=90°，
∴△ACD∽△CBD，
结合图形可得：△ACD∽△ABC、△CBD∽△ABC．
综上可得：共3对相似三角形．
故答案为：3．
点评：本题考查了相似三角形的判定，解答本题的关键是熟练掌握相似三角形的判定方法，最常用的就是两角法．
分析：根据等角的余角相等可得：∠ACD=∠CBD，利用两角法可确定图中的相似三角形．
解答：∵∠ACD+∠DCB=90°，∠CBD+∠DCB=90°，
∴∠ACD=∠CBD，
又∵∠ADC=∠CDB=90°，
∴△ACD∽△CBD，
结合图形可得：△ACD∽△ABC、△CBD∽△ABC．
综上可得：共3对相似三角形．
故答案为：3．
点评：本题考查了相似三角形的判定，解答本题的关键是熟练掌握相似三角形的判定方法，最常用的就是两角法．
练习册系列答案
相关题目
18、如图，在△ABC中，∠BAC=60°，BD、CE分别是边AC，AB上的高，BD、CE相交于点O，则∠BOC的度数是
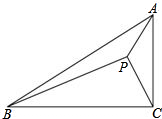如图，△ABC中，∠BAC=60°，AB=2AC．点P在△ABC内，且PA=
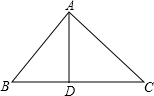如图，在△ABC中，∠BAC=90°，AB=AC=a，AD是△ABC的高，则AD的长为
93、如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BF平分∠ABC，那么△AEF是等腰三角形吗？