Question

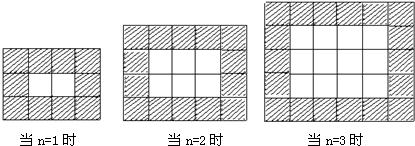
如图，用同样规格的黑白两色正方形瓷砖铺设矩形地面，请观察下列图形，探究并观察下列问题．

（1）在第4个图中，共有白色瓷砖________块；
（2）在第n个图中，共有瓷砖________块；
（3）如果每块黑瓷砖4元，每块白瓷砖3元，铺设当n=10时，共需花多少钱购买瓷砖？

Answer 1

解：（1）通过观察图形可知，当n=1时，用白瓷砖2块，黑瓷砖10块；
当n=2时，用白瓷砖6块，黑瓷砖14块；
当n=3时，用白瓷砖12块，黑瓷砖18块；
可以发现，需要白瓷砖的数量和图形数之间存在这样的关系，即白瓷砖块数等于图形数的平方加上图形数；
需要黑瓷砖的数量和图形数之间存在这样的关系，即黑瓷砖块数等于图形数的4倍加上图形数．
所以，在第n个图形中，白瓷砖的块数可用含n的代数式表示为n²+n；
黑瓷砖的块数可用含n的代数式表示为4n+6．
∴当n=4时，白色瓷砖有n²+n=16+4=20块，
故答案为20；
（2）由（1）可得总块数可表示为n²+n+4n+6=（n+3）（n+2），
故答案为（n+2）（n+3）．
（3）观察图形可知，每-横行有白砖（n+1）块，每-竖列有白砖n块，因而白砖总数是n（n+1）块，n=10时，白砖为10×11=110（块），黑砖数为46（块）．
故总钱数为110×3+46×4=330+184=514（元），
答：共花514元钱购买瓷砖．
分析：（1）通过观察发现规律，然后将n=20代入即可；
（2）将黑色瓷砖和白色瓷砖加在一起即可得到答案；
（3）求出当n=10时黑色和白色瓷砖的个数，然后计算总费用即可．
点评：此题主要考查学生对图形变化类这个知识点的理解和掌握，此题有一定拔高难度，属于难题，解答此题的关键是通过观察和分析，找出其中的规律．