题目内容
 如图,△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是△BAD的角平分线,DF∥AB交AE延长线于F,则DF的长为( )
如图,△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是△BAD的角平分线,DF∥AB交AE延长线于F,则DF的长为( )| A、4.5 | B、9 | C、5 | D、3 |
考点:等腰三角形的判定与性质,含30度角的直角三角形
专题:
分析:先求出∠C=30°,得出AD的长,再证出∠DAE=∠F,得出DF=AD即可.
解答:解:∵AB=AC=9,AD是△ABC的中线,
∴∠B=∠C=30°,AD⊥BC,∠BAD=
∠BAC=60°,
∴AD=
AB=4.5;
∵AE平分∠BAD,DF∥AB,
∴∠DAE=∠BAE=30°,∠F=∠BAE=30°,
∴∠DAE=∠F,
∴DF=AD=4.5;
故选:A.
∴∠B=∠C=30°,AD⊥BC,∠BAD=
| 1 |
| 2 |
∴AD=
| 1 |
| 2 |
∵AE平分∠BAD,DF∥AB,
∴∠DAE=∠BAE=30°,∠F=∠BAE=30°,
∴∠DAE=∠F,
∴DF=AD=4.5;
故选:A.
点评:本题考查了等腰三角形的判定与性质以及含30°角的直角三角形的性质;证明DF=AD是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
-5的倒数是( )
| A、5 | ||
B、
| ||
C、-
| ||
| D、-5 |
 如图,数轴上的点P表示的实数可能是( )
如图,数轴上的点P表示的实数可能是( )A、-
| ||
B、-2
| ||
C、-
| ||
D、2
|
抛物线y=x2+3x-4与x轴交点的个数为( )
| A、1个 | B、2个 | C、0个 | D、3个 |
一个点从数轴上的-3表示的点开始,先向右移动2个单位长度,再向左移动4个单位长度,这时该点所对应的数是( )
| A、3 | B、-5 | C、-1 | D、-9 |
 已知抛物线y=x2+bx+c的图象如图所示,则一元二次方程x2+bx+c=0的解是
已知抛物线y=x2+bx+c的图象如图所示,则一元二次方程x2+bx+c=0的解是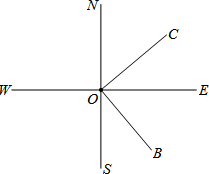 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.