题目内容
在?ABCD中,
(1)若∠A+∠C=80°,∠D=______°;
(2)若周长为40cm,AB:AD=2:3,则AB=______cm,BC=______cm.
解:(1)∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=80°,
∴∠C=40°,
∵AD∥BC,
∴∠D=180°-∠C=140°;
(2)∵?ABCD的周长为40cm,
∴AB=CD,AD=BC,
∴AB+AD=20cm,
∵AB:AD=2:3,
∴AB=8cm,AD=12cm,
∴BC=12cm.
故答案为:(1)140;(2)8,12.
分析:(1)由四边形ABCD是平行四边形,根据平行四边形的对角相等,即可求得∠A的度数,继而可求得答案;
(2)由在?ABCD的周长为40cm,AB:AD=2:3,继而可求得AB与AD的长,继而可求得BC的长.
点评:此题考查了平行四边形的性质.此题难度不大,注意掌握定理的应用是关键.
∴∠A=∠C,
∵∠A+∠C=80°,
∴∠C=40°,
∵AD∥BC,
∴∠D=180°-∠C=140°;
(2)∵?ABCD的周长为40cm,
∴AB=CD,AD=BC,
∴AB+AD=20cm,
∵AB:AD=2:3,
∴AB=8cm,AD=12cm,
∴BC=12cm.
故答案为:(1)140;(2)8,12.
分析:(1)由四边形ABCD是平行四边形,根据平行四边形的对角相等,即可求得∠A的度数,继而可求得答案;
(2)由在?ABCD的周长为40cm,AB:AD=2:3,继而可求得AB与AD的长,继而可求得BC的长.
点评:此题考查了平行四边形的性质.此题难度不大,注意掌握定理的应用是关键.

练习册系列答案
相关题目
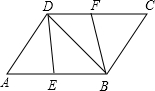 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD. 如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )
如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )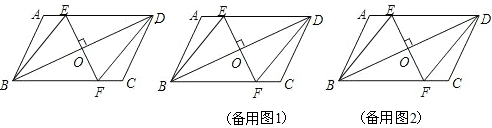
 如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.