题目内容
在平面直角坐标系 xOy中,我们把横坐标为整数、纵坐标为完全平方数的点称为“好点”,求二次函数 y=(x-90)2-4907的图象上所有“好点”的坐标.
解:设y=m2,(x-90)2=k2,m、k都是非负数,则
k2-m2=7×701=1×4907,
即(k-m)(k+m)=7×701=1×4907,
即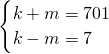 或
或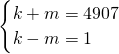 ,
,
解得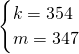 或
或 ,
,
解得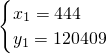 ,
,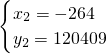 ,
,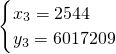 ,
,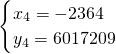 ,
,
故好点共有四个,它们的坐标为(444,120409)(-264,120409)(2544,6017209)(-2364,6017209).
分析:设y=m2,(x-90)2=k2,m、k都是非负数,可得(k+m)(k-m)=4907,把4907进行分解,然后解得m和n的值,即可求出x和y的值.
点评:本题主要考查完全平方数的知识点,解答本题的关键是设出y=m2,(x-90)2=k2,求出m和k的值即可求得好点的坐标.
k2-m2=7×701=1×4907,
即(k-m)(k+m)=7×701=1×4907,
即
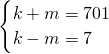 或
或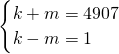 ,
,解得
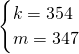 或
或 ,
,解得
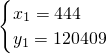 ,
,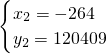 ,
,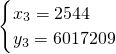 ,
,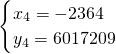 ,
,故好点共有四个,它们的坐标为(444,120409)(-264,120409)(2544,6017209)(-2364,6017209).
分析:设y=m2,(x-90)2=k2,m、k都是非负数,可得(k+m)(k-m)=4907,把4907进行分解,然后解得m和n的值,即可求出x和y的值.
点评:本题主要考查完全平方数的知识点,解答本题的关键是设出y=m2,(x-90)2=k2,求出m和k的值即可求得好点的坐标.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 12、在平面直角坐标系中,我们称边长为1且顶点的横纵坐标均为整数的正方形为单位格点正方形.如图,菱形ABCD的四个顶点坐标分别是(-8,0),(0,4),(8,0),(0,-4),则菱形ABCD能覆盖的单位格点正方形的个数是
12、在平面直角坐标系中,我们称边长为1且顶点的横纵坐标均为整数的正方形为单位格点正方形.如图,菱形ABCD的四个顶点坐标分别是(-8,0),(0,4),(8,0),(0,-4),则菱形ABCD能覆盖的单位格点正方形的个数是
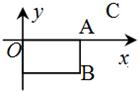 3、已知:矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,-2),则矩形的面积等于
3、已知:矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,-2),则矩形的面积等于