题目内容
 如图,半径为2
如图,半径为2| 5 |
(1)求证:PA•PB=PC•PD;
(2)若AB=8,CD=6,求OP的长.
分析:(1)连接AD,BC,易证Rt△APD∽Rt△CPB,根据相似三角形的性质,可以证得.
(2)先求出OM,ON,进而证得四边形OMPN是矩形,所以OP=PM,利用勾股定理可以求出OP.
(2)先求出OM,ON,进而证得四边形OMPN是矩形,所以OP=PM,利用勾股定理可以求出OP.
解答: 解:(1)连接AD,BC,
解:(1)连接AD,BC,
∵∠A、∠C所对的圆弧相同,
∴∠A=∠C,
∴Rt△APD∽Rt△CPB,
∴
=
,
∴PA•PB=PC•PD;
(2)作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
由垂径定理得:OM2=(2
)2-42=4,ON2=(2
)2-32=11,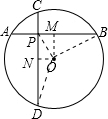
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∴OP=
=
.
 解:(1)连接AD,BC,
解:(1)连接AD,BC,∵∠A、∠C所对的圆弧相同,
∴∠A=∠C,
∴Rt△APD∽Rt△CPB,
∴
| AP |
| CP |
| PD |
| PB |
∴PA•PB=PC•PD;
(2)作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
由垂径定理得:OM2=(2
| 5 |
| 5 |

∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∴OP=
| OM2+ON2 |
| 15 |
点评:本题给出了圆中的两条相交弦,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+(
)2成立,知道这三个量中的任意两个,就可以求出另外一个.
| a |
| 2 |

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,半径为2
如图,半径为2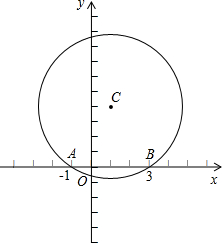 3,0)两点,且点C在x轴的上方.
3,0)两点,且点C在x轴的上方. 如图,半径为
如图,半径为 如图,半径为
如图,半径为