题目内容
【题目】已知:等边![]() 中.
中.
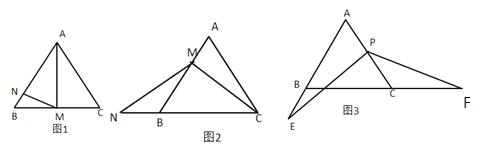
(1)如图1,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,满足
边上,满足![]() ,求
,求![]() 的值.
的值.
(2)如图2,点![]() 在
在![]() 边上(
边上(![]() 为非中点,不与
为非中点,不与![]() 、
、![]() 重合),点
重合),点![]() 在
在![]() 的延长线上且
的延长线上且![]() ,求证:
,求证:![]() .
.
(3)如图3,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,满足
的延长线上,满足![]() ,求
,求![]() 的值.
的值.
【答案】(1)3;(2)见解析;(3)![]() .
.
【解析】
(1)先证明![]() ,
,![]() 与
与![]() 均为直角三角形,再根据直角三角形中
均为直角三角形,再根据直角三角形中![]() 所对的直角边等于斜边的一半,证明BM=2BN,AB=2BM,最后转化结论可得出BN与AN之间的数量关系即得;
所对的直角边等于斜边的一半,证明BM=2BN,AB=2BM,最后转化结论可得出BN与AN之间的数量关系即得;
(2)过点M作ME∥BC交AC于E,先证明AM=ME,再证明![]() 与
与![]() 全等,最后转化边即得;
全等,最后转化边即得;
(3)过点P作PM∥BC交AB于M,先证明M是AB的中点,再证明![]() 与
与![]() 全等,最后转化边即得.
全等,最后转化边即得.
(1)∵![]() 为等边三角形,点
为等边三角形,点![]() 是
是![]() 的中点
的中点
∴AM平分∠BAC,![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴在![]() 中,
中,![]()
在![]() 中,
中,![]()
∴![]()
∴![]() 即
即![]() .
.
(2)如下图:
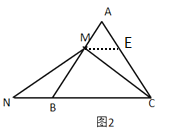
过点M作ME∥BC交AC于E
∴∠CME=∠MCB,∠AEM=∠ACB
∵![]() 是等边三角形
是等边三角形
∴∠A=∠ABC=∠ACB=![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴AM=ME
∵![]()
∴∠CME=∠MNB,MN=MC
∴在![]() 与
与![]() 中
中
∴![]()
∴![]()
∴![]()
(3)如下图:
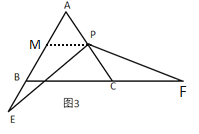
过点P作PM∥BC交AB于M
∴![]()
∵![]() 是等边三角形
是等边三角形
∴∠A=∠ABC=∠ACB=![]() ,
,![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
∴![]() 是等边三角形,
是等边三角形,![]()
∴![]()
∵P点是AC的中点
∴![]()
∴![]()
在![]() 与
与![]() 中
中
∴![]()
∴![]()
∴![]()
∴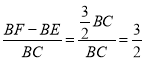 .
.

练习册系列答案
相关题目