题目内容
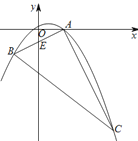
【题目】如图,抛物线![]() 过A(1,0)、B(-1,-1)、C(3,m)三点。
过A(1,0)、B(-1,-1)、C(3,m)三点。
(1)求抛物线的解析式及m的值;
(2)判断![]() 与AC的位置关系,并证明你的结论;
与AC的位置关系,并证明你的结论;
(3)在抛物线上是否存在点P,当PH![]() x轴于点H时,以P、H、A为顶点的三角形与
x轴于点H时,以P、H、A为顶点的三角形与![]() 相似?若存在,求出点P坐标;若不存在,请说明理由。
相似?若存在,求出点P坐标;若不存在,请说明理由。
【答案】(1)抛物线的解析式为![]() ,m的值为-4;
,m的值为-4;
(2)![]() ⊥AC ,证明见解析;
⊥AC ,证明见解析;
(3)存在点P共3个,分别为P1(![]() ),P2(
),P2(![]() ),P3(3,-4)或P4(
),P3(3,-4)或P4(![]() ).
).
【解析】试题分析:(1)待定系数法求解析式;
(2)利用勾股定理求得三边长,由勾股定理逆定理可探究出结论;
(3)利用三角形相似的判定转化为求方程的解而得解.
试题解析:(1)由题可知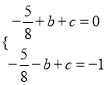 解得
解得![]()
![]()
![]() ;
;
(2)![]() ⊥AC,证明如下:
⊥AC,证明如下:
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() ⊥AC .
⊥AC .
(3)设P(![]() ),则PH=
),则PH=![]() ,
, ![]() ,
,
![]()
![]() 时,
时, ![]() ∽
∽![]() ;
;
∴![]() ,即
,即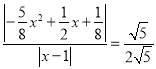 ,
,
解得![]() 或x=
或x=![]() ,
,
当![]() 时,P与A、B重合
时,P与A、B重合
![]() ,此时P(
,此时P(![]() )或P(
)或P(![]() );
);
![]()
![]() 时,
时, ![]() ∽
∽![]() ;
;
∴![]() 即
即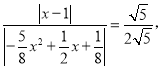
解得![]() ,
,
当x=![]() 时,与A重合
时,与A重合
![]() x=3 或
x=3 或![]() ,此时点P为P(3,-4)或P(
,此时点P为P(3,-4)或P(![]() )
)
所以存在点P共3个,分别为P1(![]() ),P2(
),P2(![]() ),P3(3,-4)或P4(
),P3(3,-4)或P4(![]() ).
).

练习册系列答案
相关题目